题目内容
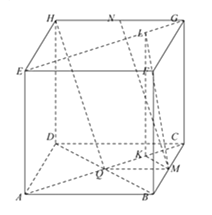
【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示，在正方体中，设BC的中点为M，GH的中点为N
(1)请将字母F，G，H标记在正方体相应的顶点处（不需说明理由）；
(2)证明：直线MN∥平面BDH
（3）求异面直线MN与AG所成角的余弦值
【答案】（1）（2）见解析；（3）
【解析】
(1) 直接将平面图形折叠同时注意顶点的对应方式即可.(2)先证明QH∥MN，再证明MN∥平面BDH.(3)先证明
就是异面直线AG与MN所成角（或其补角），再利用余弦定理求异面直线AG与MN所成角的余弦值为
.
（1）直接将平面图形折叠同时注意顶点的对应方式即可，如图
(2)连接BD，取BD的中点Q，连接MQ，
因为M，Q为线段BC、BD中点，所以MQ∥CD∥GH且
,
又因为N为GH中点，所以
得到NH=MQ且NH∥MQ，
所以四边形QMNH为平行四边形，得到QH∥MN
又
，所以MN∥平面BDH
(3)如图所示，在原正方体的右侧补上一个与其大小相等的正方体，连接GO，易得GO∥MN，
就是异面直线AG与MN所成角（或其补角），
设正方体的棱长为2，则
,
所以异面直线AG与MN所成角的余弦值为.
练习册系列答案
相关题目
【题目】某食品店为了了解气温对销售量的影响，随机记录了该店1月份中5天的日销售量
（单位：千克）与该地当日最低气温
（单位： 
）的数据，如下表：
| 2 | 5 | 8 | 9 | 11 |
| 12 | 10 | 8 | 8 | 7 |
（1）求出
与
的回归方程
；
（2）判断
与
之间是正相关还是负相关；若该地1月份某天的最低气温为6
，请用所求回归方程预测该店当日的营业额.
附: 回归方程
中， 
,
