题目内容
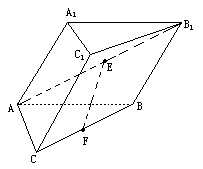
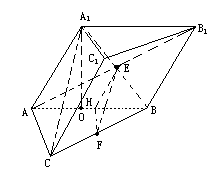
如图,已知斜三棱柱ABC—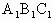 的底面是直角三角形,AC⊥CB,∠ABC=
的底面是直角三角形,AC⊥CB,∠ABC=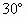 ,侧面
,侧面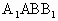 是边长为a的菱形,且垂直于底面,
是边长为a的菱形,且垂直于底面,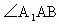 =
=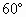 ,E、F分别是
,E、F分别是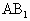 、BC的中点.
、BC的中点.
(Ⅰ)求证:EF∥侧面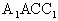 ;
;
(Ⅱ)求四棱锥A—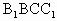 的体积;
的体积;
(Ⅲ)求EF与侧面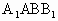 所成角的正切值.
所成角的正切值.
答案:
解析:
解析:
|
(Ⅰ)证明:连结
∵ ∴E是 又F是BC的中点, ∴EF∥ 又 ∴EF∥平面 (Ⅱ)解:∵平面 ∴在平面 则 ∴ = (Ⅲ)解:在平面ABC内,过F作FH⊥AB于H, 则FH⊥侧面 连结EH,则∠HEF为EF与侧面 在Rt△FHB中,FH= 在△HEB中,HE= 在Rt△EHF中,tan∠HEF= |

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
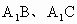 .
.
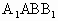 是菱形,且E是
是菱形,且E是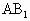 的中点,
的中点,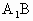 的中点.
的中点.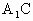 .
.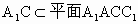 ,
, ,
,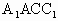 .
.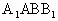 ⊥平面ABC,交线AB,
⊥平面ABC,交线AB,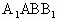 内,过
内,过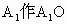 ⊥AB于O,
⊥AB于O,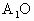 ⊥平面ABC,且h=
⊥平面ABC,且h=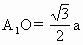 .
.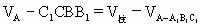
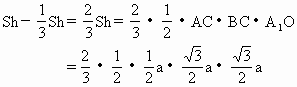
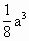 .
.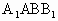 .
.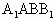 所成的角.
所成的角.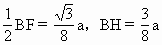 .
.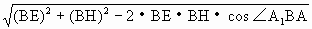
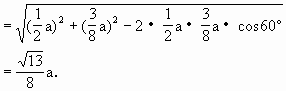
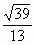 .
. (甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC=
(甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC= 如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成的角为
如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成的角为 如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为
如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为 (2011•孝感模拟)如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成的角为θ,且
(2011•孝感模拟)如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成的角为θ,且 (2012•梅州二模)如图,已知斜三棱柱ABC-A1B1C1中,点B1在底面ABC上的射影落在BC上,CA=CB=a,AB=
(2012•梅州二模)如图,已知斜三棱柱ABC-A1B1C1中,点B1在底面ABC上的射影落在BC上,CA=CB=a,AB=