题目内容
已知函数 ,
, .
.
(Ⅰ)求函数 的最小值和最小正周期;
的最小值和最小正周期;
(Ⅱ)设 的内角
的内角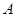 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,满足
,满足 ,
, 且
且 ,求
,求 、
、 的值.
的值.
(Ⅰ)最小值为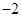 ,最小正周期为
,最小正周期为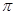 ;(Ⅱ)
;(Ⅱ)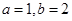 .
.
解析试题分析:(Ⅰ)将原函数化为一角一函数形式解答;(Ⅱ)由 得出
得出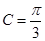 ,然后根据条件
,然后根据条件 得
得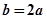 ,利用余弦定理得
,利用余弦定理得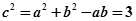 ,联立解出
,联立解出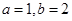 .
.
试题解析:(Ⅰ)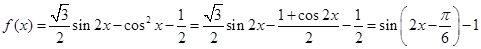 3分
3分
则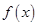 的最小值是
的最小值是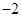 , 最小正周期是
, 最小正周期是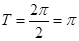 ; 6分
; 6分
(Ⅱ)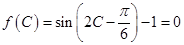 ,则
,则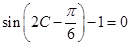 , 7分
, 7分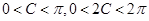 , ,所以
, ,所以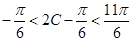 ,
,
所以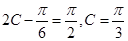 , 9分
, 9分
因为 ,所以由正弦定理得
,所以由正弦定理得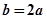 10分
10分
由余弦定理得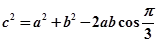 ,即
,即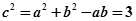 11分
11分
由①②解得: ,
,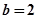 12分
12分
考点:三角函数化简、三角函数的周期、正弦定理、余弦定理.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
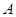 处下山至
处下山至 处有两条路径.一条是从
处有两条路径.一条是从 ,然后从
,然后从 匀速步行,速度为
匀速步行,速度为 .在甲出发
.在甲出发 后,乙从
后,乙从 后,再从
后,再从 ,索道
,索道 长为
长为 ,经测量
,经测量 ,
, .
.
 分钟,乙步行的速度应控制在什么范围内?
分钟,乙步行的速度应控制在什么范围内? 上的函数
上的函数 的图象关于直线
的图象关于直线 对称,当
对称,当 时函数
时函数 图象如图所示
图象如图所示
 的表达式;
的表达式; 的解;
的解; 的值,使得
的值,使得 在
在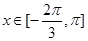 上恒成立;若存在,求出
上恒成立;若存在,求出 ,的部分图象如图所示.
,的部分图象如图所示.
 的解析式;
的解析式; .
. 的最小正周期和最大值;
的最小正周期和最大值; 为锐角,且
为锐角,且 ,求
,求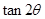 的值.
的值.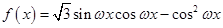 ,其中
,其中 为使
为使 能在
能在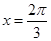 时取得最大值的最小正整数.
时取得最大值的最小正整数. 的三边长
的三边长 、
、 、
、 满足
满足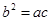 ,且边
,且边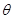 的取值集合为
的取值集合为 ,当
,当 时,求
时,求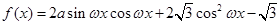
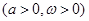 d的最大值为2,
d的最大值为2,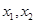 是集合
是集合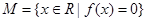 中的任意两个元素,且
中的任意两个元素,且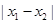 的最小值为
的最小值为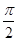 .
. 的解析式及其对称轴;
的解析式及其对称轴;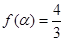 ,求
,求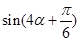 的值.
的值.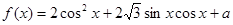 ,且当
,且当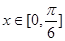 时,
时, 的最小值为2.
的最小值为2.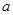 的值,并求
的值,并求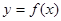 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的 倍,再把所得图象向右平移
倍,再把所得图象向右平移 个单位,得到函数
个单位,得到函数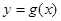 ,求方程
,求方程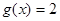 在区间
在区间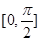 上的所有根之和.
上的所有根之和.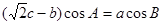 .
.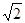 ,ΔABC的面积为1,求b,c.
,ΔABC的面积为1,求b,c.