Question

【题目】已知函数，为函数的导函数．

(1)若，函数在处的切线方程为，求a、的值；

(2)若曲线上存在两条互相平行的切线，其倾斜角为锐角，求实数的取值范围．

Answer 1

【答案】（1）；（2）0＜a＜1.

【解析】

（1）对F′（x）＝lnx+x﹣ax2，由切点为（1，﹣1），斜率为﹣2，可得和F′（1）=-2，联立解得a，b即可．

（2）令h（x）＝f′（x）＝lnx+x﹣ax2，（x＞0），h′（x）＝+1﹣2ax＝ ，令u（x）＝﹣2ax2+x+1，对a≤0和a＞0时两种情况分别讨论，即可求出．

(1)F(x)＝xln x－x＋x2－ax3＋b，F′(x)＝ln x＋x－ax2，∵切点为(1，－1)，切线斜率为k＝－2，∴∴a＝3，b＝.

所以

(2) f′（x）＝lnx+x﹣ax2，令h（x）＝f′（x）＝lnx+x﹣ax2，（x＞0），

h′（x）＝+1﹣2ax＝，

令u（x）＝﹣2ax2+x+1，

当a≤0时，u（x）＞0，∴h′（x）＞0，h（x）在（0，+∞）上单调递增，不适合题意，舍去．

当a＞0时，u（x）的△＝1+8a＞0，设方程u（x）＝0的两根分别为x1，x2，

∵x1x2＝﹣＜0，不妨设x1＜0＜x2，当x∈（0，x2）时，h′（x）＞0，当x∈（x2，+∞）时，h′（x）＜0．

∴h（x）在x∈（0，x2）时单调递增，当x∈（x2，+∞）时，h（x）单调递减．

∴，得到，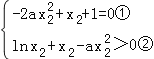

由①可得：代入②整理可得2lnx2+x2﹣1＞0③．

∵函数v（x）＝2lnx+x﹣1在（0，+∞）上单调递增，v（1）＝0，

∴x2＞1，由①可得，

∵，∴0＜2a＜2，∴0＜a＜1．