题目内容
【题目】在平行六面体ABCD—A1B1C1D1中,AB=AC,平面BB1C1C⊥底面ABCD,点M、F分别是线段AA1、BC的中点.
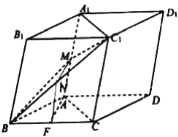
(1)求证:AF⊥DD1;
(2)求证:AF∥平面MBC1.
【答案】(1)见证明(2)见证明
【解析】
(1)由题意可得AF⊥BC.再结合平面![]() 底面
底面![]() ,得到AF⊥平面
,得到AF⊥平面![]() ,
,
可得到AF⊥CC1,根据CC1∥DD1,证得AF⊥DD1.
(2)先根据平行六面体中的线线平行,证出四边形AFEM是平行四边形,得到EM // AF,即可证明线面平行.
证明:(1)∵AB![]() AC,点F是线段BC的中点,
AC,点F是线段BC的中点,
∴AF⊥BC.又∵平面![]() 底面
底面![]() ,AF
,AF![]() 平面ABC,
平面ABC,
平面![]() 底面
底面![]() ,
,
∴AF⊥平面![]() .
.
又CC1![]() 平面
平面![]() ,∴AF⊥CC1,
,∴AF⊥CC1,
又CC1∥DD1,∴AF⊥DD1.
(2)连结B1C与BC1交于点E,连结EM,FE.
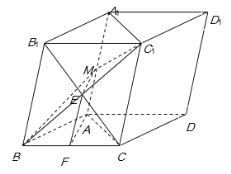
在斜三棱![]() 中,四边形BCC1B1是平行四边形,
中,四边形BCC1B1是平行四边形,
∴点E为B1C的中点.
∵点F是BC的中点,
∴FE//B1B,FE![]() B1B.
B1B.
又∵点M是平行四边形BCC1B1边AA1的中点,
∴AM//B1B,AM![]() B1B.
B1B.
∴AM// FE,AM![]() FE.
FE.
∴四边形AFEM是平行四边形.
∴EM // AF.
又EM![]() 平面MBC1,AF
平面MBC1,AF![]() 平面MBC1,
平面MBC1,
∴AF //平面MBC1.

练习册系列答案
相关题目