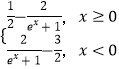题目内容
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,若函数
时,若函数![]() 在区间
在区间![]() 内单调递减,求
内单调递减,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(1)求导![]() ,对k分类讨论,得到函数的单调区间;(2)函数
,对k分类讨论,得到函数的单调区间;(2)函数![]() 在区间
在区间![]() 内单调递减,即不等式在
内单调递减,即不等式在![]() 在
在![]() 上成立,利用二次函数的图象与性质,易得
上成立,利用二次函数的图象与性质,易得![]() 的取值范围.
的取值范围.
试题解析:
(Ⅰ)函数![]() 的定义域为
的定义域为![]() .
.
![]() ,
,
(1)当![]() 时,令
时,令![]() ,解得
,解得![]() ,此时函数
,此时函数![]() 为单调递增函数;
为单调递增函数;
令![]() ,解得
,解得![]() ,此时函数
,此时函数![]() 为单调递减函数.
为单调递减函数.
(2)当![]() 时,
时,
①当![]() ,即
,即![]() 时,
时,
令![]() ,解得
,解得![]() 或
或![]() ,此时函数
,此时函数![]() 为单调递增函数;
为单调递增函数;
令![]() ,解得
,解得![]() ,此时函数
,此时函数![]() 为单调递减函数.
为单调递减函数.
②当![]() 时,
时, ![]() 恒成立,函数
恒成立,函数![]() 在
在![]() 上为单调递增函数;
上为单调递增函数;
③当![]() ,即
,即![]() 时,
时,
令![]() ,解得
,解得![]() 或
或![]() ,此时函数
,此时函数![]() 为单调递增函数;
为单调递增函数;
令![]() ,解得
,解得![]() ,此时函数
,此时函数![]() 为单调递减函数.
为单调递减函数.
综上所述,
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,
, ![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,
, ![]() ,单调递减区间为
,单调递减区间为![]() .
.
(Ⅱ)![]() ,
,
因为函数![]() 在
在![]() 内单调递减,所以不等式在
内单调递减,所以不等式在![]() 在
在![]() 上成立.
上成立.
设![]() ,则
,则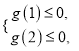 即
即![]() 解得
解得![]() .
.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
【题目】下表是某厂的产量x与成本y的一组数据:
产量x(千件) | 2 | 3 | 5 | 6 |
成本y(万元) | 7 | 8 | 9 | 12 |
(Ⅰ)根据表中数据,求出回归直线的方程 ![]() =
= ![]() x
x ![]() (其中
(其中 ![]() =
= 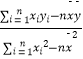 ,
, ![]() =
= ![]() ﹣
﹣ ![]() )
)
(Ⅱ)预计产量为8千件时的成本.