题目内容
已知a>b>c,且a+b+c=0,
(1)试判断 ,
, 及
及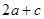 的符号;
的符号;
(2)用分析法证明 ”.
”.
(1)试判断
 ,
, 及
及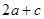 的符号;
的符号;(2)用分析法证明
 ”.
”. (1)c<0,a>0,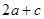 >0
>0
(2)利用分析法寻找结论成立的充分条件的运用。
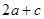 >0
>0(2)利用分析法寻找结论成立的充分条件的运用。
试题分析:(1) 解:∵a+b+c=0,a>b>c,∴
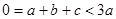 ∴a>0,
∴a>0,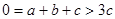 ∴c<0.
∴c<0.  4分
4分(2)要证
 成立,
成立,只需证
 a,
a,即证b2-ac<3a2,
只需证(a+c)2-ac<3a2,
即证(a-c)(2a+c)>0,
∵a-c>0,2a+c>0,
∴(a-c)(2a+c)>0成立,故原不等式成立. 8分
点评:主要是考查了不等式的证明 ,以及不等式中变量的符号的判定,属于中档题。

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
 满足
满足 ,则
,则 的最大值是
的最大值是  ,
, ,且
,且 ,那么
,那么 的取值范围是( )
的取值范围是( )
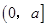


 的最大值为( )
的最大值为( ) 的最大值.
的最大值.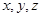 满足
满足 ,则当
,则当 取得最大值时,
取得最大值时, 的最大值为( )
的最大值为( )



 ,则
,则 的最大值为_________________.
的最大值为_________________. ,且
,且 ,则
,则 的最小值为
的最小值为  ,则
,则 的最小值是 .
的最小值是 .