题目内容
(本题满分10分)
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< )的一段图象如图所示.
)的一段图象如图所示.

(1)求f(x)的解析式;
(2)求f(x)的单调减区间,并指出f(x)的最大值及取到最大值时x的集合;
(3)把f(x)的图象向左至少平移多少个单位,才能使得到的图象对应的函数为偶函数?
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
 )的一段图象如图所示.
)的一段图象如图所示.
(1)求f(x)的解析式;
(2)求f(x)的单调减区间,并指出f(x)的最大值及取到最大值时x的集合;
(3)把f(x)的图象向左至少平移多少个单位,才能使得到的图象对应的函数为偶函数?
(1)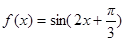 ;
;
(2)函数f(x)的单调减区间为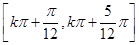 (k∈Z).
(k∈Z).
函数f(x)的最大值为1,取到最大值时x的集合为{x|x=kπ+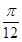 ,k∈Z}.
,k∈Z}.
(3)至少须左移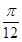 个单位才能使所对应函数为偶函数
个单位才能使所对应函数为偶函数
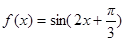 ;
;(2)函数f(x)的单调减区间为
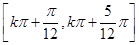 (k∈Z).
(k∈Z).函数f(x)的最大值为1,取到最大值时x的集合为{x|x=kπ+
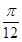 ,k∈Z}.
,k∈Z}. (3)至少须左移
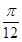 个单位才能使所对应函数为偶函数
个单位才能使所对应函数为偶函数本试题主要考查了三角函数的解析式和其图像与性质和三角函数函数图像的变换的综合运用。
(1)因为由图像可知周期,得到w,然后利用振幅得到A,代入一个特殊点得到初相的值,得到解析式。
(2)利用三角函数的图像与性质,求解三角函数的值域,并求解取得最值时自变量的取值集合
(3)根据图像的平移变换和周期变化和振幅变换可知至少要左移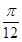 个单位,才能符合题意。
个单位,才能符合题意。
解:(1)从图知,函数的最大值为1,

则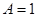 函数
函数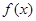 的周期为
的周期为 ,而
,而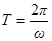 ,则
,则 ,
,
又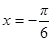 时,
时,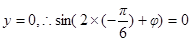 ,而
,而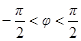 ,则
,则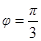 ,
,
∴函数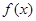 的表达式为
的表达式为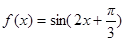 ……4分
……4分
(2)由2kπ+ ≤
≤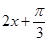 ≤2kπ+
≤2kπ+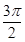 得,
得,
kπ+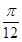 ≤x≤kπ+
≤x≤kπ+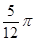 (k∈Z),
(k∈Z),
∴函数f(x)的单调减区间为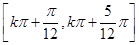 (k∈Z).
(k∈Z).
函数f(x)的最大值为1,取到最大值时x的集合为{x|x=kπ+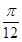 ,k∈Z}.……7分
,k∈Z}.……7分
(3)解法一:f(x)=sin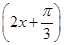
=cos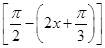 =cos
=cos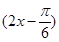
=cos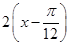 ,
,
故至少须左移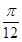 个单位才能使所对应函数为偶函数.……10分
个单位才能使所对应函数为偶函数.……10分
解法二:f(x)=sin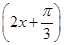 的图象的对称轴方程为
的图象的对称轴方程为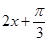 =kπ+
=kπ+ ,
,
∴x=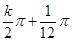 ,当k=0时,x=
,当k=0时,x=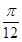 ,k=-1时,x=
,k=-1时,x=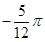 ,
,
故至少左移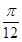 个单位.……10分
个单位.……10分
(1)因为由图像可知周期,得到w,然后利用振幅得到A,代入一个特殊点得到初相的值,得到解析式。
(2)利用三角函数的图像与性质,求解三角函数的值域,并求解取得最值时自变量的取值集合
(3)根据图像的平移变换和周期变化和振幅变换可知至少要左移
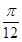 个单位,才能符合题意。
个单位,才能符合题意。解:(1)从图知,函数的最大值为1,

则
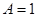 函数
函数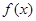 的周期为
的周期为 ,而
,而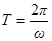 ,则
,则 ,
,又
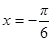 时,
时,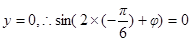 ,而
,而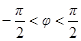 ,则
,则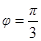 ,
,∴函数
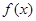 的表达式为
的表达式为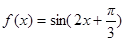 ……4分
……4分(2)由2kπ+
 ≤
≤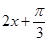 ≤2kπ+
≤2kπ+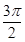 得,
得,kπ+
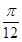 ≤x≤kπ+
≤x≤kπ+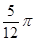 (k∈Z),
(k∈Z),∴函数f(x)的单调减区间为
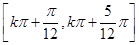 (k∈Z).
(k∈Z).函数f(x)的最大值为1,取到最大值时x的集合为{x|x=kπ+
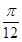 ,k∈Z}.……7分
,k∈Z}.……7分(3)解法一:f(x)=sin
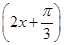
=cos
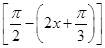 =cos
=cos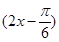
=cos
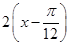 ,
,故至少须左移
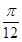 个单位才能使所对应函数为偶函数.……10分
个单位才能使所对应函数为偶函数.……10分解法二:f(x)=sin
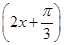 的图象的对称轴方程为
的图象的对称轴方程为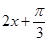 =kπ+
=kπ+ ,
,∴x=
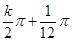 ,当k=0时,x=
,当k=0时,x=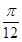 ,k=-1时,x=
,k=-1时,x=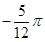 ,
,故至少左移
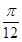 个单位.……10分
个单位.……10分
练习册系列答案
相关题目
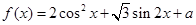 (a∈R,a为常数).
(a∈R,a为常数).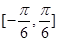 上最大值与最小值之和为3,求a的值;
上最大值与最小值之和为3,求a的值; 为坐标原点,向量
为坐标原点,向量 ,点
,点 是直线
是直线 上的一点,且点
上的一点,且点 分有向线段
分有向线段 的比为
的比为 .
.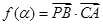 ,
, ,讨论函数
,讨论函数 的单调性,并求其值域;
的单调性,并求其值域; 三点共线,求
三点共线,求 的值.
的值. (
( )的最小正周期是
)的最小正周期是 ,若其图像向右平移
,若其图像向右平移 个单位后得到的函数为奇函数,则函数
个单位后得到的函数为奇函数,则函数 的图像
的图像 对称
对称 对称
对称 对称
对称 对称
对称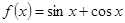
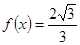 ,求sin2x的值;
,求sin2x的值;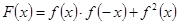 的最大值与单调递增区间.
的最大值与单调递增区间. (
( )的最小正周
)的最小正周 ,
, 的值;
的值; 的图像上各点的横坐标缩短到原来的
的图像上各点的横坐标缩短到原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数
 上的最小值.
上的最小值.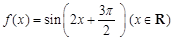 ,给出下面四个命题:①函数
,给出下面四个命题:①函数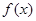 的最小正周期为
的最小正周期为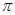 ;
;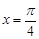 对称;④函数
对称;④函数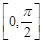 上是增函数,其中错误命题的序号是 .
上是增函数,其中错误命题的序号是 .
 的图象与x轴交点为
的图象与x轴交点为 ,相邻最高点坐标为
,相邻最高点坐标为 .
.  的表达式;
的表达式; 的单调增区间;
的单调增区间; 在
在 上的最值.
上的最值.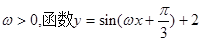 的图像向右平移
的图像向右平移 个单位后与原图像重合,则
个单位后与原图像重合,则 的最小值是( )
的最小值是( )

