题目内容
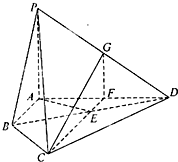
如图所示，AB是圆O的直径，PA垂直于圆O所在的平面，M是圆周上异于A、B的任意一点，AN⊥PM，点N为垂足，求证：AN⊥平面PBM．
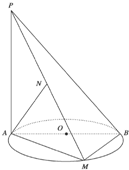
证明：∵AB是圆的直径，M是圆周上异于A、B的任意一点，
∴AM⊥BM，
∵PA⊥平面ABM，BM?平面ABM，
∴PA⊥BM．
又∵PA∩AM=A，PA?平面PAM，AC?平面PAM，
∴BM⊥平面PAM，
又∵AN?平面PAM，
∴AN⊥BM，
又∵AN⊥PM，BM∩PM=M．
∴AN⊥平面PBM．
∴AM⊥BM，
∵PA⊥平面ABM，BM?平面ABM，
∴PA⊥BM．
又∵PA∩AM=A，PA?平面PAM，AC?平面PAM，
∴BM⊥平面PAM，
又∵AN?平面PAM，
∴AN⊥BM，
又∵AN⊥PM，BM∩PM=M．
∴AN⊥平面PBM．
练习册系列答案
智能训练练测考系列答案
相关题目
