题目内容
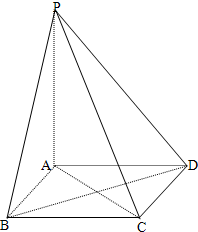
如图,边长为4的正方形ABCD所在平面与正三角形PAD所在平面互相垂直,M,Q分别为PC,AD的中点,
(1)求四棱锥P-ABCD的体积;
(2)求证:PA∥平面MBD;
(3)试问:在线段AB上是否存在一点N,使得平面PCN⊥平面PQB?若存在,试指出点N的位置,并证明你的结论;若不存在,请说明理由.
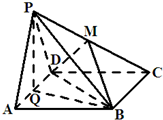
(1)求四棱锥P-ABCD的体积;
(2)求证:PA∥平面MBD;
(3)试问:在线段AB上是否存在一点N,使得平面PCN⊥平面PQB?若存在,试指出点N的位置,并证明你的结论;若不存在,请说明理由.

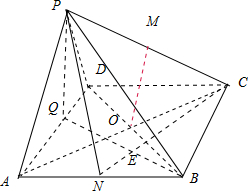
(1)连接PQ,∵PA=PD=AD=4,AQ=QD,∴PQ⊥AD,PQ=2
.
又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴PQ⊥底面ABCD.
∴V=
×42×2
=
.
(2)证明:连接AC、BD交于点O,连接OM.
则AO=OC,又PM=MC,
∴PA∥OM.
∵PA?平面BMD,OM?平面BMD,
∴PA∥平面BMD.
3)存在,N为AB中点.
证明:取AB的中点N,连接CN交BQ于点E.
由正方形ABCD可知:△ABQ≌△BCN,∴∠ABQ=∠BCN,
∵∠CNB+∠BCN=90°,∴∠ABQ+∠CNB=90°,∴BQ⊥CN.
由(1)可知:PQ⊥平面ABCD,∴PQ⊥CN.
又PQ∩QB=Q,∴CN⊥平面PQB,
∵CN?平面PCN,
∴平面PCN⊥平面PQB.
| 3 |

又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴PQ⊥底面ABCD.
∴V=
| 1 |
| 3 |
| 3 |
32
| ||
| 3 |
(2)证明:连接AC、BD交于点O,连接OM.
则AO=OC,又PM=MC,
∴PA∥OM.
∵PA?平面BMD,OM?平面BMD,
∴PA∥平面BMD.
3)存在,N为AB中点.
证明:取AB的中点N,连接CN交BQ于点E.
由正方形ABCD可知:△ABQ≌△BCN,∴∠ABQ=∠BCN,
∵∠CNB+∠BCN=90°,∴∠ABQ+∠CNB=90°,∴BQ⊥CN.
由(1)可知:PQ⊥平面ABCD,∴PQ⊥CN.
又PQ∩QB=Q,∴CN⊥平面PQB,
∵CN?平面PCN,
∴平面PCN⊥平面PQB.

练习册系列答案
相关题目