题目内容
函数
的定义域为
，若存在非零实数
使得对于任意
，有
，且
，则称为
上的高调函数。如果定义域为
的函数是奇函数，当
时，
，且为上的4高调函数，那么实数
的取值范围是
的定义域为，若存在非零实数使得对于任意，有，且，则称为上的高调函数。如果定义域为的函数是奇函数，当时，，且为上的4高调函数，那么实数的取值范围是 A． . | B． |
C． | D． |
C
解：定义域为R的函数f（x）是奇函数，
当x≥0时，
f（x）=|x-a2|-a2
的图象如图，
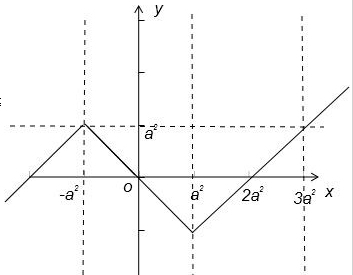
∵f（x）为R上的4高调函数，当x＜0时，函数的最大值为a2，要满足f（x+l）≥f（x），4大于等于区间长度3a2-（-a2），
∴4≥3a2-（-a2），∴-1≤a≤1，选A
当x≥0时，
f（x）=|x-a2|-a2
的图象如图，
∵f（x）为R上的4高调函数，当x＜0时，函数的最大值为a2，要满足f（x+l）≥f（x），4大于等于区间长度3a2-（-a2），
∴4≥3a2-（-a2），∴-1≤a≤1，选A
练习册系列答案
相关题目
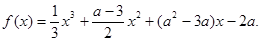
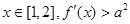恒成立，求实数a的取值范围；
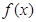的两个极值点分别为
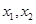判断下列三个代数式：
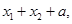②
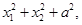③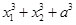
中有几个为定值？并且是定值请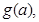求出；
并求出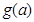
的最小值. 
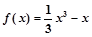在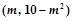
上有最小值，则实数m的取值范围是 .
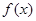在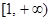
上为增函数，求正实数
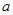的取值范围；
，求证：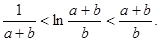
，
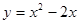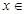[0，3]的值域是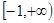
；⑤y＝cosx.其中为一阶格点函数的是________(填序号)．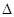
CPD的面积为
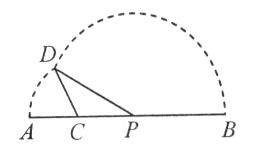
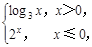，则
则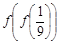
的值为_____．