题目内容
椭圆C：
+
=1的左、右顶点分别为M、N，点P在C上，且直线PN的斜率为-
，则直线PM斜率为（ ）
| x2 |
| 4 |
| y2 |
| 3 |
| 1 |
| 4 |
A、
| ||
| B、3 | ||
C、-
| ||
| D、-3 |
考点：直线与圆锥曲线的关系
专题：直线与圆,圆锥曲线的定义、性质与方程
分析：求出M，N的坐标，进而求出直线PN的方程，联立椭圆方程后，求出P点坐标，代入斜率公式，可得答案．
解答：
解：∵椭圆C：
+
=1的左、右顶点分别为M、N，
∴M点坐标为（-2，0），N点坐标为（2，0），
又∵直线PN的斜率为-
，
∴直线PN的方程为：y=-
（x-2），
代入椭圆C：
+
=1方程可得：13x2-4x-44=0，
设P点坐标为（x，y），则x+2=
，解得x=-
，y=
，
故直线PM斜率k=
=3，
故选：B
| x2 |
| 4 |
| y2 |
| 3 |
∴M点坐标为（-2，0），N点坐标为（2，0），
又∵直线PN的斜率为-
| 1 |
| 4 |
∴直线PN的方程为：y=-
| 1 |
| 4 |
代入椭圆C：
| x2 |
| 4 |
| y2 |
| 3 |
设P点坐标为（x，y），则x+2=
| 4 |
| 13 |
| 22 |
| 13 |
| 12 |
| 13 |
故直线PM斜率k=
| ||
-
|
故选：B
点评：本题考查的知识点是直线与圆锥曲线的关系，直线的斜率，难度不大，属于基础题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
函数f（x）=
，若f（0）是f（x）的最小值，则a的取值范围为（ ）
|
| A、[-1，2] |
| B、[-1，0] |
| C、[1，2] |
| D、[0，2] |
如果4sin
+3cos
=0，那么角θ的终边所在的象限是（ ）
| θ |
| 2 |
| θ |
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
定义在（-1，1）上的函数f（x）-f（y）=f（
）；当x∈（-1，0）时，f（x）＞0，若P=f（
）+f（
），Q=f（
），R=f（0），则P，Q，R的大小关系为（ ）
| x-y |
| 1-xy |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 3 |
| A、Q＞P＞R |
| B、P＞Q＞R |
| C、R＞Q＞P |
| D、R＞P＞Q |
已知平面点集M={(x，y)
}，平面点集{（x，y）|x2+y2≤1}，在集合M中任取一点P，则点P落在集合N中的概率为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
已知f（x）=
，则曲线f（x）与y=
，x轴围成的封闭图形的面积为（ ）
|
| x+2 |
| A、3 | ||||
B、
| ||||
C、
| ||||
D、
|
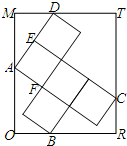如图矩形ORTM内放置5个大小相同的正方形，其中A、B、C、D都在矩形的边上，若向量