题目内容
数列{an}中,an+1=
(n∈N*),且a7=
,则a5= .
| 2an |
| 1+an |
| 1 |
| 2 |
考点:数列递推式
专题:等差数列与等比数列
分析:由于an+1=
(n∈N*),且a7=
,分别令n=6,5,即可解出.
| 2an |
| 1+an |
| 1 |
| 2 |
解答:
解:∵an+1=
(n∈N*),
∴a7=
=
,解得a6=
.
∴a6=
=
,解得a5=
.
故答案为:
.
| 2an |
| 1+an |
∴a7=
| 1 |
| 2 |
| 2a6 |
| 1+a6 |
| 1 |
| 3 |
∴a6=
| 1 |
| 3 |
| 2a5 |
| 1+a5 |
| 1 |
| 5 |
故答案为:
| 1 |
| 5 |
点评:本题考查了递推式的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
函数f(x)=
,若f(0)是f(x)的最小值,则a的取值范围为( )
|
| A、[-1,2] |
| B、[-1,0] |
| C、[1,2] |
| D、[0,2] |
已知f(x)=
,则曲线f(x)与y=
,x轴围成的封闭图形的面积为( )
|
| x+2 |
| A、3 | ||||
B、
| ||||
C、
| ||||
D、
|
已知数列{an}的前n项和Sn=n2,则a2等于( )
| A、1 | B、3 | C、4 | D、5 |
执行如图所示的程序框图,则输出的结果为( )


| A、4 | B、9 | C、7 | D、5 |
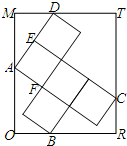 如图矩形ORTM内放置5个大小相同的正方形,其中A、B、C、D都在矩形的边上,若向量
如图矩形ORTM内放置5个大小相同的正方形,其中A、B、C、D都在矩形的边上,若向量 如图,分别以正方形ABCD的四条边为直径画半圆,重叠部分如图中阴影区域.
如图,分别以正方形ABCD的四条边为直径画半圆,重叠部分如图中阴影区域.