题目内容
由直线 上的一点向圆
上的一点向圆 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( )
| A.1 | B. | C.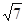 | D.3 |
C
解析试题分析:从题意看出,切线长、直线上的点到圆心的距离、半径之间满足勾股定理,显然圆心到直线的距离最小时,切线长也最小.圆心到直线的距离为: ,所以切线长的最小值为:
,所以切线长的最小值为: 。故答案为:C。
。故答案为:C。
考点:圆的切线方程;直线与圆的综合应用。
点评:此题的关键是分析出由直线 上的哪一点向圆引切线,切线长最小。考查了学生分析问题解决问题的能力。体现了转化的数学思想,是基础题.
上的哪一点向圆引切线,切线长最小。考查了学生分析问题解决问题的能力。体现了转化的数学思想,是基础题.

练习册系列答案
相关题目
圆 和圆
和圆 的位置关系为( )
的位置关系为( )
| A.相交 | B.内切 | C.外切 | D.外离 |
若 ,则直线
,则直线 被圆
被圆 所截得的弦长为( )
所截得的弦长为( )
A. | B.1 | C. | D. |
已知圆心在x轴上,半径是5且以A(5,4)为中点的弦长是2 ,则这个圆的方程是( )
,则这个圆的方程是( )
| A.(x-3)2+y2=25 | B.(x-3)2+y2=25或(x-7)2+y2=25 |
| C.(x±3)2+y2=25 | D.(x+3)2+y2=25或(x+7)2+y2=25 |
若点P(1,1)为圆 的弦MN的中点,则弦MN所在直线的方程为( )
的弦MN的中点,则弦MN所在直线的方程为( )
A. | B. |
C. | D. |
 是圆
是圆 :
: 内一点,过
内一点,过 被圆截得的弦最短的直线方程是( )
被圆截得的弦最短的直线方程是( )
A. | B. |
C. | D. |
直线 与圆
与圆 的位置关系是 ( )
的位置关系是 ( )
| A.相切 | B.相交但直线不过圆心 | C.直线过圆心 | D.相离 |
过点 作圆
作圆 的弦,其中弦长为整数的共有 ( )
的弦,其中弦长为整数的共有 ( )
| A.16条 | B.17条 | C.32条 | D.34条 |
 绕着其与
绕着其与 轴的交点逆时针旋转
轴的交点逆时针旋转 得到直线m,则m与圆
得到直线m,则m与圆 截得弦长为( )
截得弦长为( )


