题目内容
 是圆
是圆 :
: 内一点,过
内一点,过 被圆截得的弦最短的直线方程是( )
被圆截得的弦最短的直线方程是( )
A. | B. |
C. | D. |
A
解析试题分析: 化成标准方程为
化成标准方程为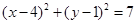 ,所以圆心为
,所以圆心为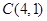 ,半径为
,半径为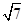 ,当
,当 所在的弦与
所在的弦与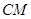 垂直时,弦长最短,而
垂直时,弦长最短,而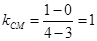 ,所以
,所以 所在的弦的斜率为
所在的弦的斜率为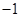 ,所以直线方程为
,所以直线方程为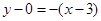 ,即
,即 .
.
考点:本小题主要考查直线与圆相交时弦的性质和两直线垂直时斜率的关系以及点斜式方程的求法,考查学生数形结合思想的运用.
点评:直线与圆相交的问题,要借助图形数形结合来解决,可以简化运算.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
若方程 表示一个圆,则有( )
表示一个圆,则有( )
A. | B.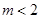 | C. | D. |
已知圆C与圆(x-1)2+y2=1关于直线y=-x对称,则圆C的方程( )
| A.(x+1)2+y2=1 | B.x2+y2=1 |
| C.x2+(y+1)2=1 | D.x2+(y-1)2=1 |
由直线 上的一点向圆
上的一点向圆 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( )
| A.1 | B. | C.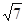 | D.3 |
若圆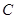 的半径为1,圆心在第一象限,且与直线
的半径为1,圆心在第一象限,且与直线 和
和 轴相切,则该圆的标准方程是 ( )
轴相切,则该圆的标准方程是 ( )
A. | B. |
C. | D. |
若直线 与曲线
与曲线 有公共点,则
有公共点,则 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
过圆 上一点
上一点 的切线方程是( )
的切线方程是( )
A. | B. | C. | D. |
以(5,6)和(3,-4)为直径端点的圆的方程是( )
A. | B. |
C. | D.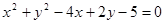 |
 与圆
与圆 有公共点
有公共点 则斜率
则斜率 的取值范围是( )
的取值范围是( )






