题目内容
已知圆心在x轴上,半径是5且以A(5,4)为中点的弦长是2 ,则这个圆的方程是( )
,则这个圆的方程是( )
| A.(x-3)2+y2=25 | B.(x-3)2+y2=25或(x-7)2+y2=25 |
| C.(x±3)2+y2=25 | D.(x+3)2+y2=25或(x+7)2+y2=25 |
B
解析试题分析:由圆心在x轴上,设圆心坐标为C(a,0),
又圆的半径r=5,弦BD长为2 ,由垂径定理得到AC垂直于弦BD,∴|CA|2+(
,由垂径定理得到AC垂直于弦BD,∴|CA|2+( )2=52,又A(5,4),∴(5-a)2+42+5=25,解得:a=3或a=7,
)2=52,又A(5,4),∴(5-a)2+42+5=25,解得:a=3或a=7,
则所求圆的方程为(x-3)2+y2=25或(x-7)2+y2=25.故选B
考点:本题主要考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,垂径定理,勾股定理,以及两点间的距离公式,当直线与圆相交时,常常根据垂径定理由垂直得中点,然后由弦长的一半,圆的半径及弦心距构造直角三角形,利用勾股定理来解决问题.
点评:解决该试题的关键是由圆心在x轴上,设出圆心C坐标为(a,0),由A为弦BD的中点,根据垂径定理得到AC垂直于BD,利用两点间的距离公式求出|AC|的长,再由圆的半径r及弦长的一半,根据勾股定理列出关于a的方程,求出方程的解得到a的值,确定出圆心的坐标,由圆心坐标及半径写出圆的标准方程即可.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
圆 :
: 与圆
与圆 :
: 的位置关系是( )
的位置关系是( )
| A.相交 | B.外切 | C.内切 | D.相离 |
以两点 和
和 为直径端点的圆的方程是
为直径端点的圆的方程是
A. | B. |
C. | D. |
已知圆C与圆(x-1)2+y2=1关于直线y=-x对称,则圆C的方程( )
| A.(x+1)2+y2=1 | B.x2+y2=1 |
| C.x2+(y+1)2=1 | D.x2+(y-1)2=1 |
直线 相切,则实数
相切,则实数 等于( )
等于( )
A. | B. | C. | D. |
由直线 上的一点向圆
上的一点向圆 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( )
| A.1 | B. | C.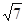 | D.3 |
若圆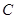 的半径为1,圆心在第一象限,且与直线
的半径为1,圆心在第一象限,且与直线 和
和 轴相切,则该圆的标准方程是 ( )
轴相切,则该圆的标准方程是 ( )
A. | B. |
C. | D. |
过圆 上一点
上一点 的切线方程是( )
的切线方程是( )
A. | B. | C. | D. |
若圆C与圆 关于原点对称,则圆C的方程是( )
关于原点对称,则圆C的方程是( )
A. | B. |
C. | D. |