题目内容
求所有的正整数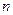 ,使得
,使得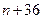 是一个完全平方数,且除了2或3以外,
是一个完全平方数,且除了2或3以外,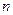 没有其他的质因数.
没有其他的质因数.
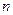 ,使得
,使得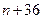 是一个完全平方数,且除了2或3以外,
是一个完全平方数,且除了2或3以外,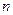 没有其他的质因数.
没有其他的质因数.符合条件的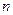 值有6个,分别为64,108,288,864,1728,10368.
值有6个,分别为64,108,288,864,1728,10368.
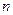 值有6个,分别为64,108,288,864,1728,10368.
值有6个,分别为64,108,288,864,1728,10368.设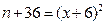 ,其中
,其中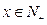 ,则
,则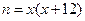 .
.
依题意,可设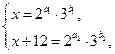 其中
其中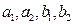 均为非负整数,于是
均为非负整数,于是
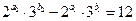 (1)…………………………5分
(1)…………………………5分
如果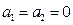 ,则
,则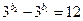 ,这是不可能的.所以
,这是不可能的.所以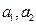 中至少有一个大于0,于是
中至少有一个大于0,于是 和
和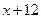 均为偶数,从而
均为偶数,从而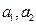 均为正整数.
均为正整数.
若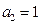 ,则
,则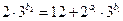 ,显然只可能
,显然只可能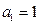 (否则左右两边被4除的余数不相同),此时
(否则左右两边被4除的余数不相同),此时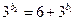 ,显然只能是
,显然只能是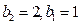 ,此时
,此时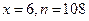 .
.
…………………………10分
若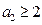 ,则
,则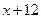 是4的倍数,从而
是4的倍数,从而 也是4的倍数,故
也是4的倍数,故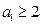 ,此时
,此时
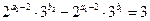 (2)
(2)
显然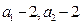 中至少有一个应为0(否则(2)式左右两边奇偶性不相同).
中至少有一个应为0(否则(2)式左右两边奇偶性不相同).
1)当 ,即
,即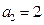 时,
时, 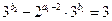 (3)
(3)
此时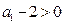 (否则等式左右两边奇偶性不相同),故
(否则等式左右两边奇偶性不相同),故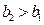 .
.
若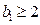 ,则(3)式左边是9的倍数,而右边为3,矛盾,故只可能
,则(3)式左边是9的倍数,而右边为3,矛盾,故只可能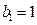 ,从而(3)式即
,从而(3)式即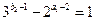 ,它只有两组解
,它只有两组解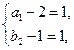 和
和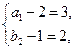 即
即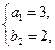 和
和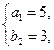 此时,对应的
此时,对应的 值分别为24和96,相应的
值分别为24和96,相应的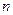 值分别为864和10368. …………………15分
值分别为864和10368. …………………15分
2)当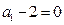 ,即
,即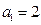 时,
时, 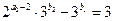 (4)
(4)
此时显然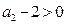 (否则等式左右两边奇偶性不相同),故
(否则等式左右两边奇偶性不相同),故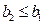 .
.
若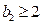 ,则(4)式左边是9的倍数,而右边是3,无解.故
,则(4)式左边是9的倍数,而右边是3,无解.故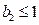 .
.
若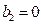 ,则
,则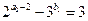 ,只可能
,只可能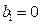 ,此时
,此时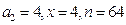 .
.
若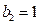 ,则(4)式即
,则(4)式即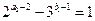 ,它只有两组解
,它只有两组解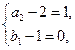 和
和 即
即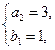 和
和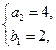 此时,对应的
此时,对应的 值分别为12和36,相应的
值分别为12和36,相应的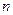 值分别为288和1728.
值分别为288和1728.
因此,符合条件的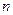 值有6个,分别为64,108,288,864,1728,10368.
值有6个,分别为64,108,288,864,1728,10368.
…………………………20分
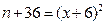 ,其中
,其中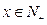 ,则
,则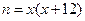 .
.依题意,可设
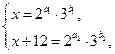 其中
其中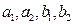 均为非负整数,于是
均为非负整数,于是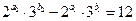 (1)…………………………5分
(1)…………………………5分如果
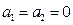 ,则
,则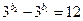 ,这是不可能的.所以
,这是不可能的.所以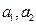 中至少有一个大于0,于是
中至少有一个大于0,于是 和
和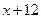 均为偶数,从而
均为偶数,从而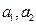 均为正整数.
均为正整数.若
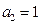 ,则
,则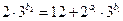 ,显然只可能
,显然只可能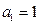 (否则左右两边被4除的余数不相同),此时
(否则左右两边被4除的余数不相同),此时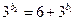 ,显然只能是
,显然只能是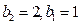 ,此时
,此时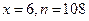 .
.…………………………10分
若
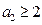 ,则
,则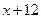 是4的倍数,从而
是4的倍数,从而 也是4的倍数,故
也是4的倍数,故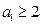 ,此时
,此时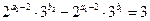 (2)
(2)显然
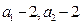 中至少有一个应为0(否则(2)式左右两边奇偶性不相同).
中至少有一个应为0(否则(2)式左右两边奇偶性不相同).1)当
 ,即
,即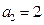 时,
时, 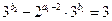 (3)
(3)此时
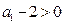 (否则等式左右两边奇偶性不相同),故
(否则等式左右两边奇偶性不相同),故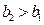 .
.若
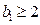 ,则(3)式左边是9的倍数,而右边为3,矛盾,故只可能
,则(3)式左边是9的倍数,而右边为3,矛盾,故只可能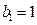 ,从而(3)式即
,从而(3)式即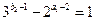 ,它只有两组解
,它只有两组解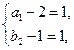 和
和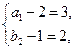 即
即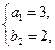 和
和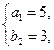 此时,对应的
此时,对应的 值分别为24和96,相应的
值分别为24和96,相应的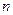 值分别为864和10368. …………………15分
值分别为864和10368. …………………15分2)当
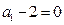 ,即
,即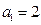 时,
时, 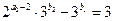 (4)
(4)此时显然
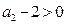 (否则等式左右两边奇偶性不相同),故
(否则等式左右两边奇偶性不相同),故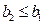 .
.若
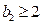 ,则(4)式左边是9的倍数,而右边是3,无解.故
,则(4)式左边是9的倍数,而右边是3,无解.故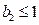 .
.若
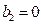 ,则
,则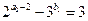 ,只可能
,只可能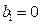 ,此时
,此时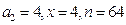 .
.若
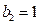 ,则(4)式即
,则(4)式即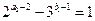 ,它只有两组解
,它只有两组解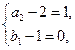 和
和 即
即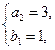 和
和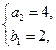 此时,对应的
此时,对应的 值分别为12和36,相应的
值分别为12和36,相应的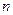 值分别为288和1728.
值分别为288和1728.因此,符合条件的
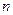 值有6个,分别为64,108,288,864,1728,10368.
值有6个,分别为64,108,288,864,1728,10368.…………………………20分

练习册系列答案
相关题目
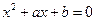 的一个根在-2与-1之间,另一个根在1与2之间,试求点
的一个根在-2与-1之间,另一个根在1与2之间,试求点 的轨迹及
的轨迹及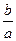 的范围.
的范围.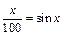 的实数解的个数为( )
的实数解的个数为( )
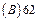
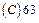
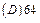
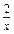 -3.
-3.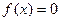 在[0,1]内的近似解,用“二分法”计算到
在[0,1]内的近似解,用“二分法”计算到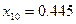 达到精确度要求。那么所取误差限
达到精确度要求。那么所取误差限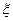 是( )
是( )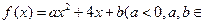 R),设关于
R),设关于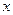 的方程
的方程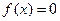 的两实根为
的两实根为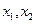 ,方程
,方程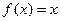 的两实根为
的两实根为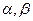 .(Ⅰ)若
.(Ⅰ)若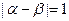 ,求
,求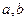 的关系式;(Ⅱ)若
的关系式;(Ⅱ)若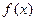 的解析式; (Ⅲ)若
的解析式; (Ⅲ)若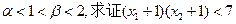 .
.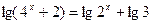 的解是
的解是 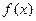 唯一的一个零点同时在区间
唯一的一个零点同时在区间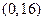 、
、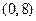 、
、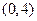 、
、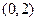 内,
内,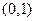 内有零点
内有零点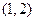 内有零点
内有零点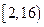 内无零点
内无零点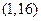 内无零点
内无零点