题目内容
设集合A={x|4x–2x+2+a=0,x∈R}.
(1)若A中仅有一个元素,求实数a的取值集合B;
(2)若对于任意a∈B,不等式x2–6x<a(x–2)恒成立,求x的取值范围.
(1)若A中仅有一个元素,求实数a的取值集合B;
(2)若对于任意a∈B,不等式x2–6x<a(x–2)恒成立,求x的取值范围.
(1) B={a|a≤0或a=4} (2)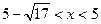
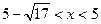
(1)令2x=t(t>0),设f(t)=t2–4t+a.
由f(t)=0在(0,+∞)有且仅有一根或两相等实根,则有
①f(t)=0有两等根时,Δ=0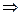 16–4a=0
16–4a=0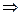 a=4
a=4
验证:t2–4t+4=0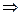 t=2∈(0,+∞),这时x=1
t=2∈(0,+∞),这时x=1
②f(t)=0有一正根和一负根时,f(0)<0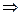 a<0
a<0
③若f(0)=0,则a=0,此时4x–4·2x=0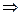 2x=0(舍去),或2x=4,∴x=2,即A中只有一个元素
2x=0(舍去),或2x=4,∴x=2,即A中只有一个元素
综上所述,a≤0或a=4,即B={a|a≤0或a=4}
(2)要使原不等式对任意a∈(–∞,0]∪{4}恒成立. 即g(a)=(x–2)a–(x2–6x)>0恒成立. 只须
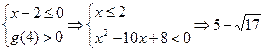 <x≤2
<x≤2
由f(t)=0在(0,+∞)有且仅有一根或两相等实根,则有
①f(t)=0有两等根时,Δ=0
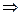 16–4a=0
16–4a=0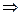 a=4
a=4验证:t2–4t+4=0
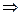 t=2∈(0,+∞),这时x=1
t=2∈(0,+∞),这时x=1②f(t)=0有一正根和一负根时,f(0)<0
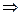 a<0
a<0③若f(0)=0,则a=0,此时4x–4·2x=0
 2x=0(舍去),或2x=4,∴x=2,即A中只有一个元素
2x=0(舍去),或2x=4,∴x=2,即A中只有一个元素综上所述,a≤0或a=4,即B={a|a≤0或a=4}
(2)要使原不等式对任意a∈(–∞,0]∪{4}恒成立. 即g(a)=(x–2)a–(x2–6x)>0恒成立. 只须
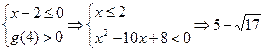 <x≤2
<x≤2
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
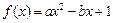 .
.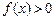 的解集是
的解集是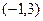 ,求实数
,求实数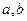 的值;
的值;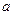 为整数,
为整数,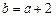 ,且函数
,且函数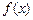 在
在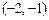 上恰有一个零点,求
上恰有一个零点,求 在区间
在区间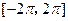 上的零点个数是( )
上的零点个数是( )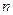 ,使得
,使得 是一个完全平方数,且除了2或3以外,
是一个完全平方数,且除了2或3以外,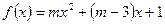 至少有一个值为正的零点,则实数
至少有一个值为正的零点,则实数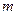 的
的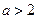 ,则函数
,则函数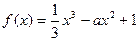 在区间
在区间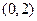 上恰好有 ( )
上恰好有 ( ) 有两个实数解,则
有两个实数解,则 的取值范围是( )
的取值范围是( )


