题目内容
求下列函数的零点：
(1)y=x3-7x+6;(2)y=x+
-3.
(1)y=x3-7x+6;(2)y=x+
-3.（1）函数y=x3-7x+6的零点为-3,1,2（2）函数y=x+-3的零点为1，2
-3的零点为1，2（1）∵x3-7x+6=(x3-x)-(6x-6)
=x(x2-1)-6(x-1)=x(x+1)(x-1)-6(x-1)
=(x-1)(x2+x-6)=(x-1)(x-2)(x+3)
解x3-7x+6=0,即(x-1)(x-2)(x+3)=0
可得x1=-3,x2=1,x3=2.
∴函数y=x3-7x+6的零点为-3,1,2.
(2)∵x+
解x+
即
=0,可得x=1或x=2.
∴函数y=x+-3的零点为1，2.
=x(x2-1)-6(x-1)=x(x+1)(x-1)-6(x-1)
=(x-1)(x2+x-6)=(x-1)(x-2)(x+3)
解x3-7x+6=0,即(x-1)(x-2)(x+3)=0
可得x1=-3,x2=1,x3=2.
∴函数y=x3-7x+6的零点为-3,1,2.
(2)∵x+
解x+
即=0,可得x=1或x=2.∴函数y=x+
-3的零点为1，2.
练习册系列答案
相关题目
存在反函数
，方程
＝0的解集是P，方程
Q；
．
在区间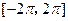
上的零点个数是（ ）
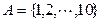，若“方程
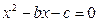满足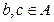
，且方程至少有一根
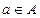”，就称该方程为“漂亮方程”。则“漂亮方程”的个数为
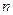，使得
是一个完全平方数，且除了2或3以外，
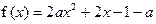在区间[-1，1]上与x轴有且只有一个交点，求：实数
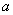的取值范围。
有两个实数解，则
的取值范围是（ ）
，其中函数
的图像是一条连续的曲线，则方程
在下面哪个区间内必有实数根 （ ）
