题目内容
定义域为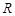 的奇函数
的奇函数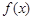 满足
满足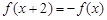 ,当
,当 时,
时,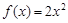 ,则
,则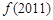 等于( )
等于( )
A.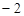 | B.0 | C.1 | D.2 |
A
解析试题分析:∵f(x)在R上是奇函数,∴函数f(-x)=-f(x),
∵f(x+2)=-f(x),所以f(x+4)=-f(x+2)=f(x)∴函数f(x) 的周期为T=4,
又f(2011)=f(502×4+3)=f(3)=f(-1)=-f(1),
∵当x∈(0,2)时,f(x)=2x2,∴f(1)=2,
故f(2011)=-f(1)=-2.
故选A。
考点:本题主要考查函数的奇偶性、周期性。
点评:典型题,利用给定结论,首先确定函数的周期性是进一步解题的关键。类似题目,均应从着手研究函数的性质开始,进一步探索解题。

练习册系列答案
相关题目
定义在R上的函数y=f(x)是增函数,且函数y=f(x-3)的图象关于点(3,0)成中心对称,若s,t满足f(s -2s) ≥-f(2t-t
-2s) ≥-f(2t-t ),则
),则
| A.s≥t | B.s<t | C.|s-1|≥|t-1| | D.s+t≥0 |
下列函数中,在其定义域内既是奇函数又是减函数的是( )
A. | B. | C. | D. |
函数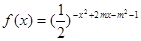 的单调增区间与值域相同,则实数
的单调增区间与值域相同,则实数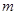 的取
的取
值为( )
A.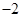 | B.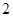 | C.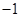 | D.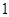 |
函数 在[0,2]上的最大值是7,则指数函数
在[0,2]上的最大值是7,则指数函数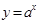 在[0,2]上的最大值与最小值的和为
在[0,2]上的最大值与最小值的和为
| A.6 | B.5 | C.3 | D.4 |
 上的函数
上的函数 是减函数,且函数
是减函数,且函数 ,
, 满足不等式
满足不等式 .则当
.则当 时,
时, 的取值范围是( )
的取值范围是( )



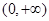 上的单调递减函数
上的单调递减函数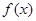 ,若
,若 ,则下列不等式成立的是( )
,则下列不等式成立的是( )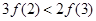
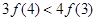
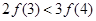
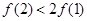
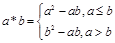 ,设
,设 ,且关于x的方程
,且关于x的方程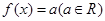 恰有三个互不相等的实数根,则实数
恰有三个互不相等的实数根,则实数 的取值范围是
的取值范围是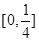
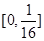

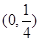
 在区间(
在区间( )的导函数
)的导函数 ,
, ,若在区间(
,若在区间( 恒成立,则称函数
恒成立,则称函数 在区间(
在区间( 若当实数
若当实数 满足
满足 时,函数
时,函数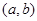 上为凸函数,则
上为凸函数,则 最大值 ( )
最大值 ( )