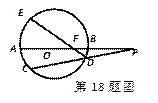题目内容
(本小题满分10分)
如图,已知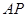 是
是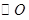 的切线,
的切线, 为切点,
为切点,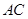 是
是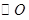 的割线,与
的割线,与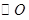 交于
交于 两点,圆心
两点,圆心 在
在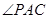 的内部,点
的内部,点 是
是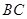 的中点.
的中点.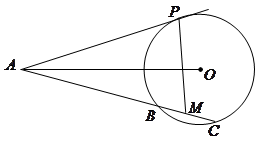
(1)证明 四点共圆;
四点共圆;
(2)求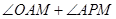 的大小.
的大小.
(1)连结 因为
因为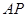 与
与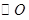 相切于点
相切于点 ,所以
,所以 .因为
.因为 是
是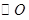 的弦
的弦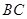 的中点,所以
的中点,所以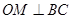 .于是
.于是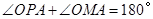 .四边形
.四边形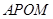 的对角互补,所以
的对角互补,所以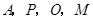 四点共圆(2)
四点共圆(2)
解析试题分析:(1)证明:连结 .
.
因为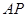 与
与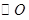 相切于点
相切于点 ,所以
,所以 .
.
因为 是
是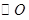 的弦
的弦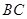 的中点,所以
的中点,所以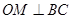 .
.
于是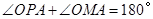 .
.
由圆心 在
在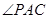 的内部,可知四边形
的内部,可知四边形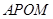 的对角互补,所以
的对角互补,所以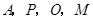 四点共圆. ……………………5分
四点共圆. ……………………5分
(2)解:由(1)得 四点共圆,所以
四点共圆,所以 .
.
由(1)得 .
.
由圆心 在
在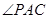 的内部,可知
的内部,可知 .
.
所以 . ……………………10分
. ……………………10分
考点:平面几何证明
点评:证明四点共圆需证四边形对角互补

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
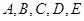 均在⊙O上,且
均在⊙O上,且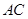 为⊙O的直径。
为⊙O的直径。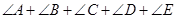 的值;
的值;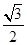 ,
, 与
与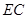 交于点
交于点 ,且
,且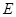 、
、 为弧
为弧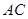 的三等分点,求
的三等分点,求 的长.
的长.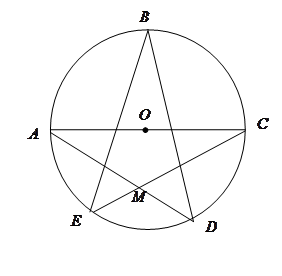
 是圆
是圆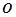 的直径,
的直径,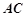 是弦,
是弦, ,垂足为
,垂足为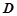 ,
,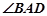 。
。
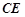 与圆
与圆 。
。
 ;
;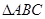 的外接圆的切线
的外接圆的切线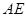 与
与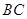 的延长线交于点
的延长线交于点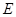 ,
,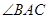 的平分线与
的平分线与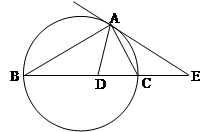
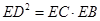
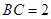 ,
, =1.求
=1.求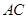 长.
长.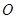 上的两点,且CF=CB,过C作CD^AF交AF的延长线与点D.
上的两点,且CF=CB,过C作CD^AF交AF的延长线与点D.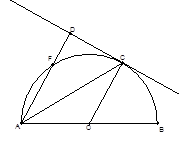

 中,
中, ,
,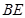 平分
平分 交
交 于点
于点 ,点
,点 在
在 上,
上, .
.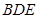 的外接圆的切线;
的外接圆的切线;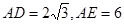 ,求
,求 的长.
的长.
 如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,A为弧CE的重点,DE交AB于点F,且AB=2BP=4,求PF的长度。
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,A为弧CE的重点,DE交AB于点F,且AB=2BP=4,求PF的长度。