题目内容
(本小题满分10分)
如图,⊙O内切于△ABC的边于D,E,F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G。
(1)求证:圆心O在直线AD上;
(2)求证:点C是线段GD的中点。
(1)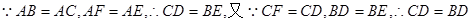
又△ABC是等腰三角形,所以AD是∠CAB的角分线
∴圆心O在直线AD上。(2))连接DF,由(I)知,DH是⊙O的直径, ∴∠DFH=90°,∴∠FDH+∠FHD=90°,又∠G+∠FHD=90°,∴∠FDH=∠G,又⊙O与AC相切于点F ,∴∠AFH=∠GCF=∠FHD ∴∠GCF=∠G,∴CG=CF=CD,∴点C是线段GD的中点。
解析试题分析:(I)证明: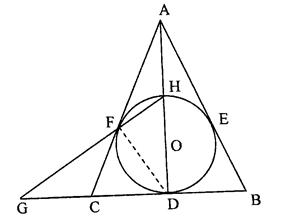
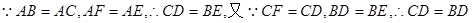
又△ABC是等腰三角形,所以AD是∠CAB的角分线
∴圆心O在直线AD上。……………5分
(II)连接DF,由(I)知,DH是⊙O的直径,
∴∠DFH=90°,∴∠FDH+∠FHD=90°
又∠G+∠FHD=90°,∴∠FDH=∠G
又⊙O与AC相切于点F
∴∠AFH=∠GCF=∠FHD ∴∠GCF=∠G
∴CG=CF=CD
∴点C是线段GD的中点。 ………………10分
考点:圆的切线的性质定理证明。
点评:本题利用了切线的性质,四边形的内角和为360度及圆周角定理求解.属于基础题型。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
曲线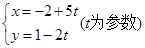 与坐标轴的交点是( )
与坐标轴的交点是( )
A.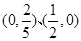 | B.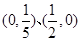 | C.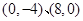 | D.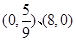 |
 AE=DC
AE=DC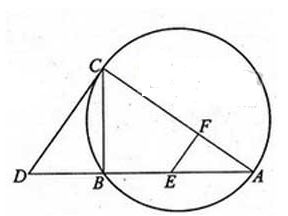

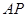 是
是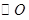 的切线,
的切线, 为切点,
为切点,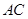 是
是 两点,圆心
两点,圆心 在
在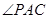 的内部,点
的内部,点 是
是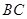 的中点.
的中点.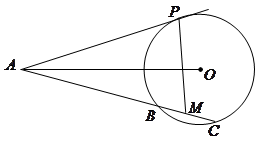
 四点共圆;
四点共圆;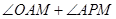 的大小.
的大小.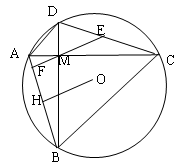
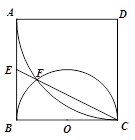
 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心,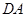 为半径的圆弧与以
为半径的圆弧与以 为直径的半圆
为直径的半圆 交于点
交于点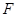 ,延长
,延长 交
交 于
于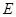 .
.
 的长.
的长. 外一点
外一点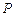 作圆
作圆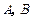 ,
,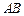 与
与 交于点
交于点 ,设
,设 为过点
为过点 四点共圆.
四点共圆.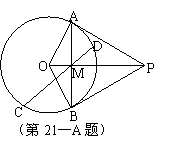

 、
、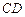 是圆
是圆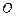 的两条弦,且
的两条弦,且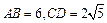 ,求线段
,求线段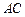 的长度.
的长度.