题目内容
设m、n是两条不同的直线,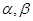 是两个不同的平面,则下列命题中正确的是
是两个不同的平面,则下列命题中正确的是
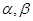 是两个不同的平面,则下列命题中正确的是
是两个不同的平面,则下列命题中正确的是A.若m∥n,m  ,则n∥ ,则n∥ ; ; | B.若 ⊥β,m∥ ⊥β,m∥ ,则m⊥β; ,则m⊥β; |
C.若 ⊥β,m⊥β,则m∥ ⊥β,m⊥β,则m∥ ; ; | D.若m⊥n,m⊥ ,n⊥β,则 ,n⊥β,则 ⊥β ⊥β |
D
试题分析:A不正确,m∥n,m?α,由于n可能在α内,故推不出n∥α;
对于B,由于当满足
 ⊥β,m∥
⊥β,m∥ ,则m与β可能斜交,因此错误
,则m与β可能斜交,因此错误对于C,由于;
 ⊥β,m⊥β,则m∥
⊥β,m⊥β,则m∥ ,也可能m在
,也可能m在 内,错误
内,错误对于D,则根据m⊥n,m⊥
 ,n⊥β,则
,n⊥β,则 ⊥β,符合面面垂直的判定定理,成立,故选D.
⊥β,符合面面垂直的判定定理,成立,故选D.点评:本题考查线面,线线、面面的平行关系的判断,重点考查了空间的感知能力与空间中线面之间位置关系的判断能力.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
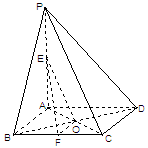
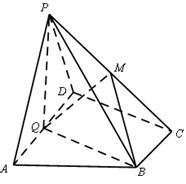
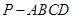 中,
中,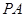 ⊥平面
⊥平面 ,
,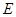 为
为 为
为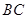 的中点,底面
的中点,底面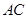 ,
, 交于点
交于点 .
.
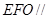 平面
平面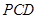 ;
; ⊥平面
⊥平面 .
.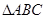 中,
中,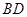 为
为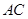 边上的高,
边上的高, ,沿
,沿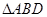 翻折,使得
翻折,使得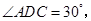 得几何体
得几何体

 ;
; AD=1,CD=
AD=1,CD=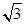 .
.
 α,且n∥α;(2)一定存在平面α,使m
α,且n∥α;(2)一定存在平面α,使m
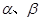 表示两个互相垂直的平面,
表示两个互相垂直的平面,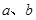 表示一对异面直线,则
表示一对异面直线,则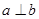 的一个充分条件是( )
的一个充分条件是( )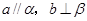 B.
B.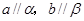
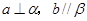 D.
D.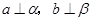
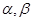 为使互不重合的平面,
为使互不重合的平面,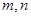 是互不重合的直线,给出下列四个命题:
是互不重合的直线,给出下列四个命题:


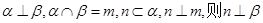 ;
;