题目内容
1．如果存在实数x使不等式|x+2|-|x-1|＜k成立，则实数k的取值范围是（-3，+∞）．分析 设f（x）=|x+2|-|x-1|，由绝对值不等式的性质，可得f（x）的最小值，由题意可得，k＞f（x）的最小值即可．
解答 解：设f（x）=|x+2|-|x-1|，
则|f（x）|≤|（x+2）-（x-1）|=3，
即有-3≤f（x）≤3，
当x≤-2时，取得最小值-3，
由存在实数x使不等式|x+2|-|x-1|＜k成立，
可得k＞f（x）的最小值，
即为k＞-3．
故答案为：（-3，+∞）．
点评 本题考查绝对值不等式的性质的运用，考查不等式成立的条件，属于中档题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
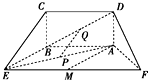如图所示的五面体中，四边形ABCD是矩形，AD⊥平面ABEF，AB∥EF，且AD=1，AB=$\frac{1}{2}$EF=2$\sqrt{2}$，AF=BE=2，点P、Q、M分别为AE、BD、EF的中点．
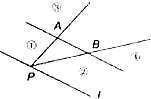如图，点P是直线l上一点，l∥直线AB，如果存在实数x，y，使得$\overrightarrow{PC}=x\overrightarrow{PA}+y\overrightarrow{PB}$，且x+y=2，x＞2，则点C所在的区域是图中标示的区域（ ）
16．设a1，a2，…an是正整数1，2，3，…，n的一个排列，令bj表示排在j的左边且比j大的数的个数，称为j的逆序数．如在排列3，5，1，4，2，6中，5的逆序数是0，2的逆序数是3，则由1至8这8个数字构成的所有排列中，满足1的逆序数是2，2的逆序数是3，5的逆序数是3的不同排列种数是（ ）
| A． | 144 | B． | 172 | C． | 180 | D． | 192 |
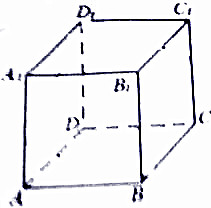如图正方体中，E、F、G分别是AA1、CC1、BB1的中点 （1）求证：B、E、D1、F四点共面（2）求证：面A1C1G∥面BED1F．
13．下列说法中正确的序号为（ ）
| A． | 若直线l平行于平面α内的无数条直线，则l∥α； | |
| B． | 若α∥β，a?α，b?β，则a与b是异面直线； | |
| C． | 若α∥β，a?α，则a∥β； | |
| D． | 若α∩β=b，a?α，则a与β一定相交． |