题目内容
17．
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（ ）| A． | 2$\sqrt{5}$ | B． | 2$\sqrt{6}$ | C． | 4$\sqrt{2}$ | D． | 4$\sqrt{3}$ |
分析 根据几何体的三视图，得出该几何体是棱长为4的正方体中的四面体，画出图形，求出它最长的棱长即可．
解答 解：
依据多面体的三视图，画出它的直观图，如图所示；
在棱长为4的正方体中，四面体ABCD就是满足图中三视图的多面体，
其中A、B点为所在棱的中点，
所以，四面体ABCD最长的棱长为
|AB|=$\sqrt{{4}^{2}{+4}^{2}}$=4$\sqrt{2}$．
故选：C．
点评 本题考查了空间几何体三视图的应用问题，也考查了空间想象能力的应用问题，是基础题目．
练习册系列答案
名题金卷系列答案
优加精卷系列答案
相关题目
7．设a，b是空间中的两条不同的直线，α，β是两个不同的平面，则a⊥b的一个充分条件是（ ）
| A． | a?α，b⊥β，α∥β | B． | a⊥α，b⊥β，α∥β | C． | a∥α，b∥β，α⊥β | D． | a?α，b∥β，α⊥β |
5．若tanθ=1，则sin2θ的值为（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | 1 | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
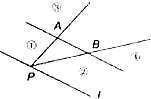如图，点P是直线l上一点，l∥直线AB，如果存在实数x，y，使得$\overrightarrow{PC}=x\overrightarrow{PA}+y\overrightarrow{PB}$，且x+y=2，x＞2，则点C所在的区域是图中标示的区域（ ）
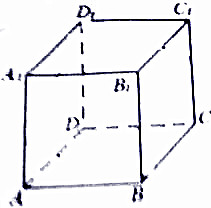如图正方体中，E、F、G分别是AA1、CC1、BB1的中点 （1）求证：B、E、D1、F四点共面（2）求证：面A1C1G∥面BED1F．