题目内容
18.已知正三棱锥的高为3cm,一个侧面三角形的面积为6$\sqrt{3}$cm2,则这个正三棱锥的侧面和底面所成的二面角的大小是60°.分析 设正三棱锥为S-ABC,底面为正三角形,高OS,O点为△ABC外(内心、重心),延长CO交AB于D,易证AB⊥CD,SD⊥AB,则∠CDS是正三棱锥的侧面和底面所成的二面角,在三角形CDP中求出此角即可.
解答  解:设正三棱锥为S-ABC,底面为正三角形,高OS,O点为△ABC外(内心、重心),延长AO交BC于D,
解:设正三棱锥为S-ABC,底面为正三角形,高OS,O点为△ABC外(内心、重心),延长AO交BC于D,
设底面边长为:a,则OD=$\frac{1}{3}×\frac{\sqrt{3}}{2}a$=$\frac{\sqrt{3}}{6}a$.
SO=3,SD=$\sqrt{{3}^{2}+(\frac{\sqrt{3}}{6}a)^{2}}$=$\sqrt{9+\frac{{a}^{2}}{12}}$,侧面三角形的面积为6$\sqrt{3}$cm2,
∴$\frac{1}{2}a•\sqrt{9+\frac{{a}^{2}}{12}}=6\sqrt{3}$,解得a=6.
SD=$\sqrt{9+3}$=2$\sqrt{3}$,OD=$\sqrt{3}$,AD⊥CB,SD⊥BC,∠SDO是S-BC-A二面角的平面角,
cos∠SDO=$\frac{1}{2}$,∠CDP=60°,侧面与底面所成的二面角是60°.
故答案为:60°.
点评 本题主要考查了二面角的平面角及求法,同时考查了正三棱锥的性质,解题的关键是寻找二面角的平面角,属于基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
13.下列说法中正确的序号为( )
| A. | 若直线l平行于平面α内的无数条直线,则l∥α; | |
| B. | 若α∥β,a?α,b?β,则a与b是异面直线; | |
| C. | 若α∥β,a?α,则a∥β; | |
| D. | 若α∩β=b,a?α,则a与β一定相交. |
1.已知等差数列{an}中,a4+a7=42,则前10项和S10=( )
| A. | 420 | B. | 380 | C. | 210 | D. | 140 |
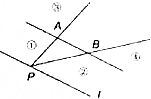 如图,点P是直线l上一点,l∥直线AB,如果存在实数x,y,使得$\overrightarrow{PC}=x\overrightarrow{PA}+y\overrightarrow{PB}$,且x+y=2,x>2,则点C所在的区域是图中标示的区域( )
如图,点P是直线l上一点,l∥直线AB,如果存在实数x,y,使得$\overrightarrow{PC}=x\overrightarrow{PA}+y\overrightarrow{PB}$,且x+y=2,x>2,则点C所在的区域是图中标示的区域( )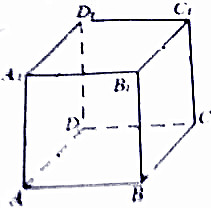 如图正方体中,E、F、G分别是AA1、CC1、BB1的中点 (1)求证:B、E、D1、F四点共面(2)求证:面A1C1G∥面BED1F.
如图正方体中,E、F、G分别是AA1、CC1、BB1的中点 (1)求证:B、E、D1、F四点共面(2)求证:面A1C1G∥面BED1F.