题目内容
已知函数 ,(
,(  为常数,
为常数, 为自然对数的底).
为自然对数的底).
(1)当 时,求
时,求 ;
;
(2)若 在
在 时取得极小值,试确定
时取得极小值,试确定 的取值范围;
的取值范围;
(3)在(2)的条件下,设由 的极大值构成的函数为
的极大值构成的函数为 ,将
,将 换元为
换元为 ,试判断曲线
,试判断曲线 是否能与直线
是否能与直线 (
( 为确定的常数)相切,并说明理由.
为确定的常数)相切,并说明理由.
 ,(
,(  为常数,
为常数, 为自然对数的底).
为自然对数的底).(1)当
 时,求
时,求 ;
;(2)若
 在
在 时取得极小值,试确定
时取得极小值,试确定 的取值范围;
的取值范围;(3)在(2)的条件下,设由
 的极大值构成的函数为
的极大值构成的函数为 ,将
,将 换元为
换元为 ,试判断曲线
,试判断曲线 是否能与直线
是否能与直线 (
( 为确定的常数)相切,并说明理由.
为确定的常数)相切,并说明理由.(1)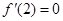 ;(2)
;(2)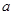 的取值范围是
的取值范围是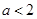 ;(3)曲线
;(3)曲线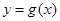 不能与直线
不能与直线 相切,证明详见解析.
相切,证明详见解析.
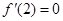 ;(2)
;(2)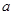 的取值范围是
的取值范围是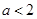 ;(3)曲线
;(3)曲线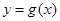 不能与直线
不能与直线 相切,证明详见解析.
相切,证明详见解析.试题分析:(1)当
 时,根据函数的求导法则求出导函数
时,根据函数的求导法则求出导函数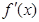 ,进而可求出
,进而可求出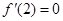 ;(2)先根据函数的求导法则求出导函数
;(2)先根据函数的求导法则求出导函数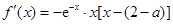 ,进而分
,进而分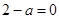 、
、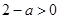 、
、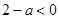 三种情况进行讨论,确定哪一种情况才符合
三种情况进行讨论,确定哪一种情况才符合 在
在 时取得极小值,进而可确定
时取得极小值,进而可确定 的取值范围;(3)根据(2)确定函数
的取值范围;(3)根据(2)确定函数 的极大值为
的极大值为 ,进而得出
,进而得出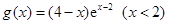 ,该曲线能否与直线
,该曲线能否与直线 相切,就看方程
相切,就看方程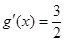 有没有解,进而转化为求函数
有没有解,进而转化为求函数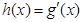 的最值问题,利用函数的导数与最值的关系进行求解判断即可.
的最值问题,利用函数的导数与最值的关系进行求解判断即可.试题解析:(1)当
 时,
时,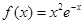 ,
,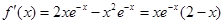
所以
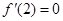
(2)因为

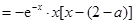
令
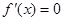 ,得
,得 或
或
当
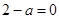 ,即
,即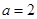 时,
时,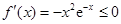 恒成立
恒成立此时
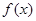 在区间
在区间 上单调递减,没有极小值;
上单调递减,没有极小值;当
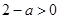 ,即
,即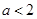 时, 若
时, 若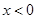 ,则
,则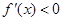 ,若
,若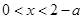 ,则
,则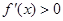
所以
 是函数
是函数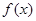 的极小值点
的极小值点当
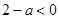 ,即
,即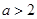 时,若
时,若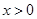 ,则
,则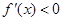 .若
.若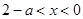 ,则
,则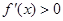
此时
 是函数
是函数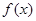 的极大值点
的极大值点综上所述,使函数
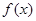 在
在 时取得极小值的
时取得极小值的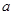 的取值范围是
的取值范围是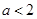
(3)由(2)知当
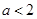 ,且
,且 时,
时,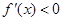
因此
 是
是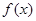 的极大值点,极大值为
的极大值点,极大值为
所以
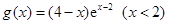 .
.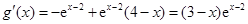
令
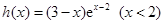
则
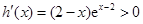 恒成立,即
恒成立,即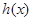 在区间
在区间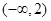 上是增函数
上是增函数所以当
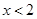 时,
时,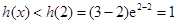 ,即恒有
,即恒有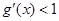
又直线
 的斜率为
的斜率为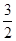
所以曲线
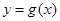 不能与直线
不能与直线 相切.
相切.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,函数
,函数 .
. 时,函数
时,函数 的图象与函数
的图象与函数 的图象有公共点,求实数
的图象有公共点,求实数 的最大值;
的最大值; 时,试判断函数
时,试判断函数 的上方?若能,求出
的上方?若能,求出 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.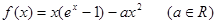 .
.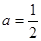 时,求函数
时,求函数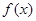 的单调区间;
的单调区间;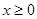 时
时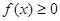 ,求a的取值范围.
,求a的取值范围.
 若当0
若当0 时,
时, 恒成立,则实数m的取值范围是 ( )
恒成立,则实数m的取值范围是 ( )
 .
. 的方程f(x)=a在区间
的方程f(x)=a在区间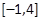 上有两个根,求a的取值范围.
上有两个根,求a的取值范围. x2.
x2.