题目内容
【题目】已知椭圆的中心在原点,焦点为![]() ,且离心率为
,且离心率为 ![]() .
.
(1)求椭圆的方程;
(2)直线(与坐标轴 不平行)与椭圆交于不同的两点,且线段中点的横坐标为![]() ,求直线倾斜角的取值范围.
,求直线倾斜角的取值范围.
【答案】
(1)
【解答】(1)设椭圆方程为![]() .焦点为(0,
.焦点为(0, ![]() ),
),![]() ,所以a=3,c=
,所以a=3,c= ![]() ,所以b=1.故所求椭圆方程为 .
,所以b=1.故所求椭圆方程为 .![]() .
.
(2)
【解答】设直线的方程为y=kx+b,代入椭圆方程 ![]() 整理得(k2+9)x2+2kb+b2-9=0,设A(x1,y1)B(x2,y2) ,且线段AB中点的横坐标为
整理得(k2+9)x2+2kb+b2-9=0,设A(x1,y1)B(x2,y2) ,且线段AB中点的横坐标为 ![]() ,由题意得
,由题意得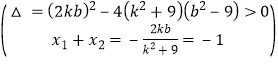 解得
解得![]() 或
或![]() .
.
又直线与坐标轴不平行,故直线倾斜角的取值范围是![]() .
.
【解析】本题考查直线与圆锥曲线的位置关系、椭圆方程的求解,考查学生分析解决问题的能力,(Ⅱ)中由直线交椭圆于不同两点得不等式△>0,由中点横坐标得一方程,两者联立即可求得范围,称为“方程不等式法”,解题中注意应用.

练习册系列答案
相关题目