Question

【题目】设函数f(x)＝|2x＋1|－|x－4|.

(1)解不等式f(x)>2；

(2)若函数f(x)≥m恒成立,求m的最大整数值．

Answer 1

【答案】（1）见解析；（2）1；（3）．

【解析】试题分析：

（1）利用绝对值的定义去绝对值符号，化函数为分段函数形式，然后分段解不等式可得结论，也可作出函数的图象与直线，从图象观察出不等式的解；

（2）作出函数图象可求得的最小值，从而可得的范围，在其中取最大整数

试题解析：

(1)令y＝|2x＋1|－|x－4|，则

y＝

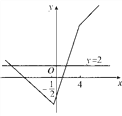
作出函数y＝|2x＋1|－|x－4|的图像，它与直线y＝2的交点为(－7,2)和(，2)．

所以|2x＋1|－|x－4|>2的解集为(－∞，－7)∪(，＋∞)．

(2)由函数y＝|2x＋1|－|x－4|的图像可知，当x＝－时，y＝|2x＋1|－|x－4|取得最小值－. 由题m<=-9/2,故m的最大整数值-5．