题目内容
【题目】如图,四棱锥![]() 的底面为菱形 且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=
的底面为菱形 且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=![]() ,
,
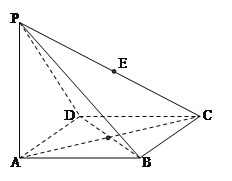
(1)求证:平面PBD⊥平面PAC;
(2)求三棱锥P--BDC的体积。
(3)在线段PC上是否存在一点E,使PC⊥平面EBD成立.如果存在,求出EC的长;如果不存在,请说明理由。
【答案】(1)见解析;(2)1;(3)![]() .
.
【解析】试题分析:
(1)要证面面垂直,一般先证线面垂直,也即要证线线垂直,由菱形可得![]() ,又由
,又由![]() 平面
平面![]() 得
得![]() ,从而可得直线与平面
,从而可得直线与平面![]() 垂直,从而得证面面垂直;
垂直,从而得证面面垂直;
(2)三棱锥![]() 的底面是
的底面是![]() ,高为
,高为![]() ,由体积公式可得体积;
,由体积公式可得体积;
(3)假设存在,由线面垂直可得线线垂直,设![]() ,则
,则![]() ,在
,在![]() 中由相似三角形可求得
中由相似三角形可求得![]() 长,反之只要有
长,反之只要有![]() ,就可得
,就可得![]() 平面
平面![]() .
.
试题解析:
(1) 略证:![]() 通过证BD⊥AC,BD⊥PA,得出BD⊥平面PAC,又BD在平面PBD内,所以平面PBD⊥平面PAD
通过证BD⊥AC,BD⊥PA,得出BD⊥平面PAC,又BD在平面PBD内,所以平面PBD⊥平面PAD
(2) ![]()
(3)假设存在,设![]() ,则
,则![]()
![]() ,Δ
,Δ![]() ∽ΔCPA ,
∽ΔCPA , ![]() .
.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
【题目】根据以往的经验,某工程施工期间的降水量![]() (单位:
(单位:![]() )对工期的影响如下表:
)对工期的影响如下表:
降水量 |
|
|
|
|
工期延误天数 | 0 | 2 | 6 | 10 |
历年气象资料表明,该工程施工期间降水量![]() 小于300,700,900的概率分别为0.3,0.7,0.9,求:
小于300,700,900的概率分别为0.3,0.7,0.9,求:
(1)工期延误天数![]() 的均值与方差;
的均值与方差;
(2)在降水量![]() 至少是300的条件下,工期延误不超过6天的概率.
至少是300的条件下,工期延误不超过6天的概率.