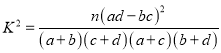题目内容
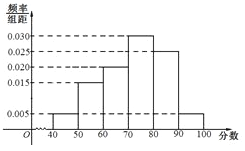
【题目】上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中抽取80名学生的数学成绩(均为整数)的频率分布直方图如图所示.
(Ⅰ)估计这次月考数学成绩的平均分和众数;
(Ⅱ)假设抽出学生的数学成绩在![]() 段各不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数字中任意抽取2个数,有放回地抽取3次,记这3次抽取中恰好有两名学生的数学成绩的次数为
段各不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数字中任意抽取2个数,有放回地抽取3次,记这3次抽取中恰好有两名学生的数学成绩的次数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
【答案】(1)平均分![]() ,众数
,众数![]() 分;(2)分布列见解析,期望
分;(2)分布列见解析,期望![]() .
.
【解析】试题分析:(1)利用中值估算抽样学生的平均分;(2)求出两个数恰好是两个学生的数学成绩的概率,确定随机变量![]() 的可能取值,求出相应的概率,可求
的可能取值,求出相应的概率,可求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
试题解析:(1)平均分![]()
![]()
![]() 分.
分.
众数的估计值是75分.
(2)在![]() 段的人数
段的人数![]() (人),
(人),
设每次抽取两个数恰好是两名学生的成绩的概率为![]() ,则
,则![]() ,
,
显然, ![]() 的可能取值为0,1,2,3.
的可能取值为0,1,2,3. ![]() ,
, ![]()
![]()
![]()
![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]()
![]() ,
,![]()

练习册系列答案
相关题目
【题目】根据以往的经验,某工程施工期间的降水量![]() (单位:
(单位:![]() )对工期的影响如下表:
)对工期的影响如下表:
降水量 |
|
|
|
|
工期延误天数 | 0 | 2 | 6 | 10 |
历年气象资料表明,该工程施工期间降水量![]() 小于300,700,900的概率分别为0.3,0.7,0.9,求:
小于300,700,900的概率分别为0.3,0.7,0.9,求:
(1)工期延误天数![]() 的均值与方差;
的均值与方差;
(2)在降水量![]() 至少是300的条件下,工期延误不超过6天的概率.
至少是300的条件下,工期延误不超过6天的概率.