题目内容
10.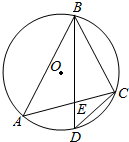 如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于E.
如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于E.(Ⅰ)若DE=2,BE=4,试求DC的值;
(Ⅱ)在(Ⅰ)的条件下,O到AC的距离为1,求⊙O的半径r.
分析 (I)先证明△BCD∽△CED,可得$\frac{DE}{DC}=\frac{DC}{DB}$,从而问题得证;
(II)OD⊥AC,设垂足为F,求出CF2=r2-1,利用DC2=CF2+DF2,建立方程,即可求得⊙O的半径.
解答 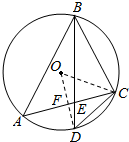 (I)证明:连接OD,OC,由已知D是弧AC的中点,可得∠ABD=∠CBD.
(I)证明:连接OD,OC,由已知D是弧AC的中点,可得∠ABD=∠CBD.
∵∠ABD=∠ECD
∴∠CBD=∠ECD
∵∠BDC=∠EDC
∴△BCD∽△CED,∴$\frac{DE}{DC}=\frac{DC}{DB}$,
∴CD2=DE•DB,
∵DE=2,BE=4,
∴DC=2$\sqrt{3}$; …(5分)
(Ⅱ)解:∵D是弧AC的中点,
∴OD⊥AC,设垂足为F,OF=1,
在Rt△COF中,OC2=CF2+OF2,即CF2=r2-1
在Rt△CFD中,DC2=CF2+DF2,
∴12=r2-1+(r-1)2,解得r=3 …(10分)
点评 本题是选考题,考查几何证明选讲,考查三角形的相似与圆的性质,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.已知随机变量X的取值为0,1,2,若P(X=0)=$\frac{1}{5}$,EX=1,则DX=( )
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
5.若x∈R,那么$\frac{x}{x+1}$是正数的充要条件是( )
| A. | x>0 | B. | x<-1 | C. | x>0或x<-1 | D. | -1<x<0 |
2.下列判断不正确的是( )
| A. | 若ξ-B(4,0.25),则Eξ=1 | |
| B. | 命题“?x∈R,x2≥0”的否定是“?x0∈R,x02<0” | |
| C. | 从匀速传递的产品生产线上,检查人员每隔5分钟从中抽出一件产品检查,这样的抽样是系统抽样 | |
| D. | 10名工人某天生产同一零件,生产的件数分别是15,17,14,10,15,17,17,16,14,12,这组数据的中位数与众数相等 |
19.如果复数$\frac{2-bi}{1+2i}$的实部和虚部互为相反数,则实数b=( )
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
20.若等式(2x-1)2014=a0+a1x+a2x2+…+a2014x2014对于一切实数x都成立,则a0+$\frac{1}{2}a$1+$\frac{1}{3}$a2+…+$\frac{1}{2015}$a2014=( )
| A. | $\frac{1}{4030}$ | B. | $\frac{1}{2015}$ | C. | $\frac{2}{2015}$ | D. | 0 |
 如图,某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道(直角△EFG,E是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口E是AB的中点,F,G分别落在AD,BC上,且AB=20m,AD=10$\sqrt{3}$m,设∠GEB=θ.
如图,某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道(直角△EFG,E是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口E是AB的中点,F,G分别落在AD,BC上,且AB=20m,AD=10$\sqrt{3}$m,设∠GEB=θ.