题目内容
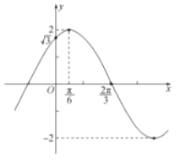
【题目】已知函数![]() 的图象如图所示,令
的图象如图所示,令![]() ,则下列关于函数
,则下列关于函数![]() 的说法中不正确的是( )
的说法中不正确的是( )
A. 函数![]() 图象的对称轴方程为
图象的对称轴方程为![]()
B. 函数![]() 的最大值为
的最大值为![]()
C. 函数![]() 的图象上存在点
的图象上存在点![]() ,使得在
,使得在![]() 点处的切线与直线
点处的切线与直线![]() :
:![]() 平行
平行
D. 方程![]() 的两个不同的解分别为
的两个不同的解分别为![]() ,
,![]() ,则
,则![]() 最小值为
最小值为![]()
【答案】C
【解析】
根据函数f(x)的图象求出A、T、ω和![]() 的值,写出f(x)的解析式,求出f′(x),写出g(x)=f(x)+f′(x)的解析式,再判断题目中的选项是否正确.
的值,写出f(x)的解析式,求出f′(x),写出g(x)=f(x)+f′(x)的解析式,再判断题目中的选项是否正确.
根据函数f(x)=Asin(ωx+![]() )的图象知,
)的图象知,
A=2,![]() ,
,
∴T=2π,ω![]() 1;
1;
根据五点法画图知,
当x![]() 时,ωx+
时,ωx+![]() ,
,
∴![]() ,
,
∴f(x)=2sin(x![]() );
);
∴f′(x)=2cos(x![]() ),
),
∴g(x)=f(x)+f′(x)
=2sin(x![]() )+2cos(x
)+2cos(x![]() )
)
=2![]() sin(x
sin(x![]() )
)
=2![]() sin(x
sin(x![]() );
);
令x![]() kπ,k∈Z,
kπ,k∈Z,
解得x![]() kπ,k∈Z,
kπ,k∈Z,
∴函数g(x)的对称轴方程为x![]() kπ,k∈Z,A正确;
kπ,k∈Z,A正确;
当x![]() 2kπ,k∈Z时,函数g(x)取得最大值2
2kπ,k∈Z时,函数g(x)取得最大值2![]() ,B正确;
,B正确;
g′(x)=2![]() cos(x
cos(x![]() ),
),
假设函数g(x)的图象上存在点P(x0,y0),使得在P点处的切线与直线l:y=3x﹣1平行,
则k=g′(x0)=2![]() cos(x0
cos(x0![]() )=3,
)=3,
解得cos(x0![]() )
)![]() 1,显然不成立,
1,显然不成立,
所以假设错误,即C错误;
方程g(x)=2,则2![]() sin(x
sin(x![]() )=2,
)=2,
∴sin(x![]() )
)![]() ,
,
∴x![]() 2kπ或x
2kπ或x![]() 2kπ,k∈Z;
2kπ,k∈Z;
∴方程的两个不同的解分别为x1,x2时,
|x1﹣x2|的最小值为![]() ,D正确.
,D正确.
故选:C.

练习册系列答案
相关题目

