题目内容
已知数列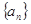 中,
中,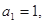 且点
且点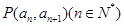 在直线
在直线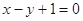 上。
上。
(1)求数列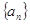 的通项公式;
的通项公式;
(2)若函数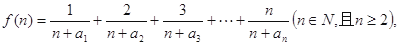 求函数
求函数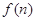 的最小值;
的最小值;
(3)设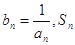 表示数列
表示数列 的前项和.试问:是否存在关于
的前项和.试问:是否存在关于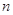 的整式
的整式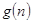 ,使得
,使得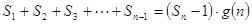 对于一切不小于2的自然数
对于一切不小于2的自然数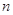 恒成立?若存在,写出
恒成立?若存在,写出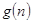 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
(1) ="n" (2)
="n" (2)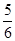 (3)存在,证明详见解析
(3)存在,证明详见解析
解析试题分析:(1)把点P(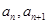 )代入直线xy1=0得到
)代入直线xy1=0得到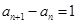 ,可知数列{
,可知数列{ }是等差数列.最后写出等差数列的通项公式
}是等差数列.最后写出等差数列的通项公式 =n.(2)首先求出
=n.(2)首先求出 的表达式,通过判断
的表达式,通过判断 的符号,确定
的符号,确定 的单调性,从而求出最小值.(3)求出
的单调性,从而求出最小值.(3)求出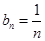 ,Sn的表达式,可得
,Sn的表达式,可得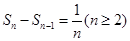 ,
,
由该递推公式可得到 ,
,
即 ,故
,故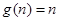 .
.
试题解析:(1)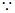 点P(
点P(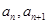 )在直线xy1=0上,即
)在直线xy1=0上,即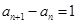 且a1=1,
且a1=1,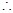 数列{
数列{ }是以1为首项,1为公差的等差数列.(2)
}是以1为首项,1为公差的等差数列.(2)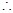
 =n(
=n( )a1=1满足
)a1=1满足 =n,所以数列
=n,所以数列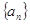 的通项公式为
的通项公式为 =n.
=n.
(2)
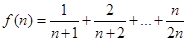

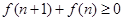
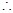
 是单调递增,故
是单调递增,故 的最小值是
的最小值是
(3)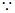
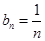
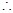
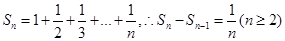 ,
,
即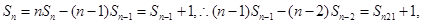 ,
,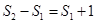
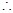

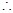

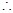
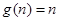 .
.
故存在关于n的整式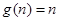 使等式对一切不小于2的自然数n恒成立.
使等式对一切不小于2的自然数n恒成立.
考点:1.等差数列的通项公式;2.数列的前n项和和增减性;3.数列的递推公式

练习册系列答案
相关题目
 …
…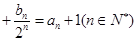 ,求{bn}的前n项和.
,求{bn}的前n项和. 的前n项和.
的前n项和.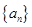 的前
的前 项和为
项和为 ,且满足
,且满足 ,其中
,其中 、
、 、
、 是常数.
是常数. ,
, ,
, ,求数列
,求数列 ,
, ,
, ,且
,且 ,求数列
,求数列 的等比数列.
的等比数列. 年,普通型汽车的总耗资费
年,普通型汽车的总耗资费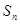 (万元)的表达式
(万元)的表达式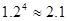
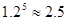
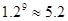
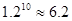 )
) 的集合:①对任意
的集合:①对任意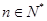 ,
,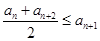 恒成立;②对任意
恒成立;②对任意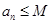 恒成立.
恒成立.
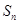 是其前n项和,且
是其前n项和,且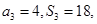 试探究数列
试探究数列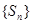 与集合W之间的关系;
与集合W之间的关系; 的通项公式为
的通项公式为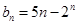 ,且
,且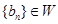 ,求M的取值范围.
,求M的取值范围.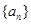 的前6项和为60,且
的前6项和为60,且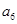 为
为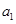 和
和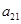 的等比中项.
的等比中项. 满足
满足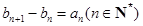 ,且
,且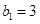 ,求数列
,求数列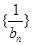 的前
的前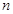 项和
项和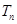 .
.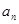 }中,
}中, ,公比
,公比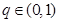 ,且
,且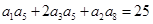 ,
,  与
与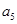 的等比中项为2.
的等比中项为2.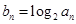 ,求:数列{
,求:数列{ }的前
}的前 项和为
项和为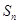 ,
,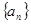 ,
,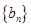 的通项
的通项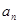 ,
,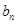 满足关系
满足关系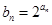 ,且数列
,且数列 项和
项和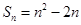
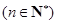 .
.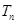 .
.