题目内容
我国于2010年10月1日成功发射嫦娥二号卫星,卫星飞行约两小时到达月球,到达月球以后,经过几次变轨将绕月球以椭圆型轨道飞行,其轨迹是以月球的月心为一焦点的椭圆。若第一次变轨前卫星的近月点到月心的距离为m,远月点到月心的距离为n,第二次变轨后两距离分别为2m,2n.则第一次变轨前的椭圆离心率比第二次变轨后的椭圆离心率 ( )
| A.变大 | B.变小 | C.不变 | D.与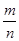 的大小有关 的大小有关 |
C
将月球的球心作为焦点,再由“卫星近月点到月心的距离为m,远月点到月心的距离为n”和“二次变轨后两距离分别为2m,2n”,可得到a+c,a-c,分别求得a,c,再求离心率后比较即得.
解:设长半轴为a,半焦距为c
第一次变轨前:
根据题意: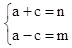
∴
∴e=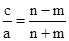
同理,第二次变轨后,椭圆离心率e=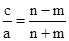
则第一次变轨前的椭圆离心率比第二次变轨后的椭圆离心率不变
故选C.
解:设长半轴为a,半焦距为c
第一次变轨前:
根据题意:
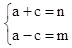
∴

∴e=
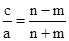
同理,第二次变轨后,椭圆离心率e=
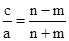
则第一次变轨前的椭圆离心率比第二次变轨后的椭圆离心率不变
故选C.

练习册系列答案
相关题目
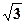 ,求此椭圆的标准方程。
,求此椭圆的标准方程。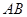 是长度为定值的平面
是长度为定值的平面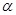 的斜线段,点
的斜线段,点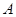 为斜足,若点
为斜足,若点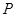 在平面
在平面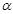 内运动,使得
内运动,使得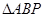 的面积为定值,则动点P的轨迹是
的面积为定值,则动点P的轨迹是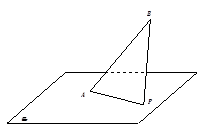
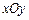 中,
中,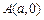
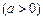 ,
,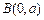 ,
,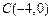 ,
,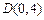 ,设
,设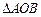 的外接圆圆心为E.
的外接圆圆心为E.
 (1)若⊙E与直线CD相切,求实数a的值;
(1)若⊙E与直线CD相切,求实数a的值;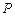 在圆
在圆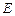 上,使
上,使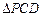 的面积等于12的点
的面积等于12的点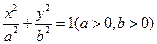 的右顶点为
的右顶点为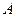 ,点
,点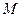 在椭圆上,且它的横坐标为1,点
在椭圆上,且它的横坐标为1,点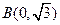 ,且
,且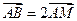 .
.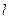 与椭圆交于另一点
与椭圆交于另一点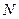 ,若线段
,若线段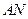 的垂直平分线经过点
的垂直平分线经过点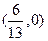 ,求直线
,求直线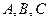 三点在
三点在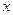 轴上,原点
轴上,原点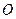 和点
和点 分别是线段
分别是线段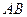 和
和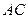 的中点,已知
的中点,已知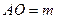 (
( 为常数),平面上的点
为常数),平面上的点 满
满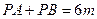 。
。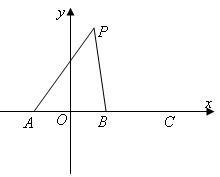
 的方程;
的方程;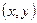 在曲线
在曲线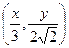 一定在某圆
一定在某圆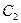 上;
上;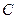 作直线
作直线 ,与圆
,与圆 两点,若点
两点,若点 恰好是线段
恰好是线段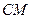 的中点,试求直线
的中点,试求直线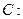
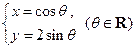 经过点
经过点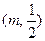 ,则
,则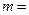 ______,离心率
______,离心率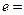 ______.
______.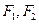 ,离心率为
,离心率为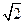 ,且过点
,且过点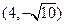 ,
,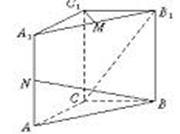
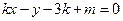 (其中
(其中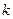 为参数)所过的定点
为参数)所过的定点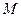 恰在双曲线上,求证:
恰在双曲线上,求证: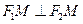 。
。 :“椭圆
:“椭圆 的焦点在x轴上” ,命题
的焦点在x轴上” ,命题 :只有一个实数
:只有一个实数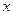 满足不等式
满足不等式 . 若命题“p且q”是真命题,求实数a的值
. 若命题“p且q”是真命题,求实数a的值 .
.