题目内容

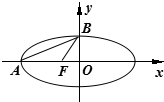
已知椭圆E：
x2
a2
+
y2
b2
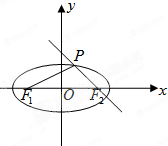
=1(a＞b＞0)的一个顶点到其左、右两个焦点F1，F2的距离分别为5和1；点P是椭圆上一点，且在x轴上方，直线PF2的斜率为-
15
．
（Ⅰ）求椭圆E的方程；
（Ⅱ）求△F1PF2的面积．
（Ⅰ）设P（x，y），F1（-c，0），F2（c，0），则a-c=1，a+c=5
∴a=3，c=2
∴b=
a2-c2
=
5

∵P到其左、右两个焦点F1，F2的距离分别为5和1，且在x轴上方，直线PF2的斜率为-
15
．
∴
(x+c)2+y2
=5
(x-c)2+y2
=1
y
x-c
=-
15
y＞0
，∴
x=
385
-1
8
c=
385
+1
8
y=
15
4

∵P到其左、右两个焦点F1，F2的距离分别为5和1，∴2a=6，∴a=3
∴b2=a2-c2=
75-
385
8

∴椭圆E的方程为
x2
9
+
y2
75-
385
8
=1；
（Ⅱ）△F1PF2的面积=
1
2
×2c×y=
385
+1
8
×
15
4
=
5
231
+
15
32
．
练习册系列答案
相关题目
设椭圆C：
x2
a2
+
y2
2
=1(a＞0)的左右焦点分别为F1、F2，A是椭圆C上的一点，且
AF2
•
F1F2
=0，坐标原点O到直线AF1的距离为
1
3
|OF1|．
（1）求椭圆C的方程；
（2）设Q是椭圆C上的一点，过点Q的直线l交x轴于点F（-1，0），交y轴于点M，若|MQ|=2|QF|，求直线l的斜率．
如图，函数y=f（x）的图象是中心在原点、焦点在x轴上的椭圆的两段弧，则不等式f（x）＜f（-x）+x的解集为（　　）
A．{x|-
2
＜x＜0或
2
＜x≤2}		B．{x|-2≤x＜-
2
或
2
＜x≤2}
C．{x|-2≤x＜-
2
2
或
2
2
＜x≤2}		D．{x|-
2
＜x＜
2
，且x≠0}
已知椭圆的一个焦点为F1（-3，0），长轴长为10，中心在坐标原点，则此椭圆的离心率为______．
如图，椭圆的标准方程为
x2
a2
+
y2
b2
=1(a＞b＞0)，P为椭圆上的一点，且满足PF1⊥PF2，
（1）求三角形PF1F2的面积．
（2）若此椭圆长轴为8，离心率为
3
2
，求点P的坐标．
如图，已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的左顶点为A，左焦点为F，上顶点为B，若∠BAO+∠BFO=90°，则该椭圆的离心率是______．
F1，F2是椭圆
x2
9
+
y2
7
=1的两个焦点，A为椭圆上一点，且∠AF1F2=45°，则三角形AF1F2的面积为（　　）
A．7B．
7
4
C．
7
2
D．
7
5
2
中心在原点，准线方程为y=±5，离心率为
5
5
的椭圆方程为（　　）
A．
x2
4
+
y2
5
=1		B．
x2
5
+
y2
4
=1		C．
x2
4
+
y2
3
=1		D．
x2
3
+
y2
4
=1
椭圆x2+2y2=6的离心率为（　　）
A．
2
B．
2
2
C．
1
2
D．
3
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网