题目内容

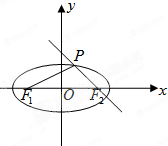
F1，F2是椭圆
x2
9
+
y2
7
=1的两个焦点，A为椭圆上一点，且∠AF1F2=45°，则三角形AF1F2的面积为（　　）
A．7B．
7
4
C．
7
2
D．
7
5
2
由题意可得 a=3，b=
7
，c=
2
，故 F1F2=2
2
，AF1+AF2=6，AF2=6-AF1，
∵AF22=AF12+F1F22-2AF1•F1F2cos45°=AF12-4AF1+8，
∴（6-AF1）2=AF12-4AF1+8，AF1=
7
2
，故三角形AF1F2的面积S=
1
2
×
7
2
×2
2
×
2
2
=
7
2
．
练习册系列答案
相关题目
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左右焦点分别为F1，F2，若△AF1F2为正三角形且周长为6；
（1）求椭圆C的标准方程；
（2）若椭圆C上存在A，B两点关于直线y=x+m对称，求实数m的取值范围；
（3）若直线l：y=kx+n与椭圆C交于A，B两点（A，B不是左右顶点），且以AB为直径的圆过椭圆C的右顶点，求证直线l过定点，并求出定点坐标．
椭圆
x2
36
+
y2
20
=1的离心率e是（　　）
A．
5
3
B．
3
2
C．
3
5
5
D．
2
3
已知椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)的一个顶点到其左、右两个焦点F1，F2的距离分别为5和1；点P是椭圆上一点，且在x轴上方，直线PF2的斜率为-
15
．
（Ⅰ）求椭圆E的方程；
（Ⅱ）求△F1PF2的面积．
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0），A、B是椭圆上的两点，线段AB的垂直平分线与x轴相交于点P（x0，0）．证明-
a2-b2
a
＜x0＜
a2-b2
a
．
若方程
x2
a
-
y2
b
=1表示焦点在y轴上的椭圆，则下列关系成立的是（　　）
A．
-b
＞
a
B．
-b
＜
a
C．
b
＞
-a
D．
b
＜
-a
曲线
x2
36
+
y2
9
=1与曲线
x2
36-k
+
y2
9-k
=1(k＜9)的（　　）
A．长、短轴相等B．准线相等
C．离心率相等D．焦距相等
已知椭圆
x2
16
+
y2
9
=1的左、右焦点分别为F1、F2，P是椭圆上的一点，Q是PF1的中点，若|OQ|=1，则|PF1|=______．
如图，F1、F2分别是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，A是椭圆C的顶点，B是直线AF2与椭圆C的另一个交点，∠F1AF2=60°．
（Ⅰ）求椭圆C的离心率；
（Ⅱ）已知△AF1B的面积为40
3
，求a，b的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网