题目内容
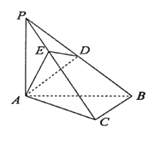
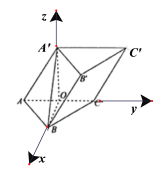
【题目】如图,三棱柱![]() 的棱长均为2,O为AC的中点,平面A'OB⊥平面ABC,平面
的棱长均为2,O为AC的中点,平面A'OB⊥平面ABC,平面![]() ⊥平面ABC.
⊥平面ABC.
(1)求证:A'O⊥平面ABC;
(2)求二面角A﹣BC﹣C'的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由已知可得AC⊥BO,平面A'OB⊥平面ABC,可证AC⊥平面BOA′,进而证明AC⊥A′O,再由面![]() ⊥平面ABC.,即可证明结论;
⊥平面ABC.,即可证明结论;
(2)以O为原点建立空间直角坐标系,求出![]() 坐标,求出平面
坐标,求出平面![]() 法向量坐标,取平面ABC的法向量为
法向量坐标,取平面ABC的法向量为![]() (0,0,1),根据空间向量面面角公式,即可求解.
(0,0,1),根据空间向量面面角公式,即可求解.
(1)证明:∵三棱柱ABC﹣A'B'C'的棱长均为2,
O为AC的中点,∴AC⊥BO,
∵平面A'OB⊥平面ABC,平面A'OB∩平面ABC=OB,
![]() 平面ABC,∴AC⊥平面BOA′,
平面ABC,∴AC⊥平面BOA′,
![]() 平面BOA′,∴AC⊥A′O,
平面BOA′,∴AC⊥A′O,
∵平面AA'C'C⊥平面ABC,平面AA'C'C∩平面ABC=AC.
![]() 平面
平面![]() ,∴A'O⊥平面ABC.
,∴A'O⊥平面ABC.
(2)解:由(1)得A'O⊥平面ABC,因为![]() 平面ABC,所以A'O⊥
平面ABC,所以A'O⊥![]() .
.
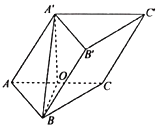
以O为原点,OB为x轴,OC为y轴,OA′为z轴,
建立空间直角坐标系,则A(0,﹣1,0),B(![]() ,0,0),
,0,0),
C(0,1,0),C′(0,2,![]() ),
),
![]() (
(![]() ,1,0),
,1,0),![]() (
(![]() ,2,
,2,![]() ),
),
设平面BCC′的法向量![]() (x,y,z),
(x,y,z),
则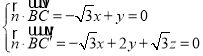 ,
,
取x=1,则![]() ,得
,得![]() (1,
(1,![]() ,﹣1),
,﹣1),
平面ABC的法向量![]() (0,0,1),
(0,0,1),
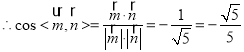 .
.
∴二面角A﹣BC﹣C'的余弦值为![]() .
.

练习册系列答案
相关题目