题目内容
【题目】如图,在三棱锥P﹣ABC中,PA⊥平面ABC,AB⊥BC,PA=AB,D为PB中点,PC=3PE.
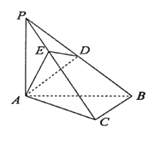
(1)求证:平面ADE⊥平面PBC;
(2)在AC上是否存在一点M,使得MB∥平面ADE?若存在,请确定点M的位置,并说明理由.
【答案】(1)证明见解析(2)存在,![]() 是
是![]() 中点;证明见解析
中点;证明见解析
【解析】
(1)根据已知可得![]() ,
,![]() ,可证BC⊥平面PAB,进而BC⊥AD,根据已知可得AD⊥PB,AD⊥平面PBC,即可证明结论;
,可证BC⊥平面PAB,进而BC⊥AD,根据已知可得AD⊥PB,AD⊥平面PBC,即可证明结论;
(2)存在M是AC中点时,MB∥平面ADE,取EC中点F,连结BM,MF,可证
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,进而证明平面
,进而证明平面![]() 平面
平面![]() ,即可证明结论.
,即可证明结论.
(1)证明:∵PA⊥平面ABC,![]() 平面ABC,∴BC⊥PA,
平面ABC,∴BC⊥PA,
![]() 平面PAB,
平面PAB,
∴BC⊥平面PAB,![]() 平面PAB,∴BC⊥AD,
平面PAB,∴BC⊥AD,
∵PA=AB,D为PB中点,∴AD⊥PB,
![]() 平面
平面![]() ,∴AD⊥平面PBC,
,∴AD⊥平面PBC,
∵AD平面ADE,∴平面ADE⊥平面PBC.
(2)点M是AC中点时,MB∥平面ADE,证明如下:
取EC中点F,连结BM,MF,
因为![]() 分别为
分别为![]() 的两个三等分点,
的两个三等分点,
在![]() 中,
中,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,
,
同理![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.

练习册系列答案
相关题目