题目内容
1.设x,y,z≥0,且x+y+z=1,求证:$\sqrt{16-48yz-15{x}^{2}}$+$\sqrt{16-48zx-15{y}^{2}}$+$\sqrt{16-48xy-15{z}^{2}}$≥9.分析 利用“分析法”证明:根据对称性,要证明:$\sqrt{16-48yz-15{x}^{2}}$+$\sqrt{16-48zx-15{y}^{2}}$+$\sqrt{16-48xy-15{z}^{2}}$≥9.只需要证明:$\sqrt{16-48yz-15{x}^{2}}$≥3,$\sqrt{16-48zx-15{y}^{2}}$≥3,$\sqrt{16-48xy-15{z}^{2}}$≥3成立.即15(x2+y2+z2)+48(zx+xy+yz)≤21.即xy+yz+zx≤$\frac{1}{3}$.由(x+y+z)2=x2+y2+z2+2(xy+yz+zx)≥3(xy+yz+zx),即可得出xy+yz+zx≤$\frac{1}{3}$成立.
解答 证明:根据对称性,要证明:$\sqrt{16-48yz-15{x}^{2}}$+$\sqrt{16-48zx-15{y}^{2}}$+$\sqrt{16-48xy-15{z}^{2}}$≥9.
只需要证明:$\sqrt{16-48yz-15{x}^{2}}$≥3,$\sqrt{16-48zx-15{y}^{2}}$≥3,$\sqrt{16-48xy-15{z}^{2}}$≥3成立.
16-48yz-15x2≥9,16-48zx-15y2≥9,16-48xy-15z2≥9.
即48yz+15x2≤7,48zx+15y2≤7,48xy+15z2≤7.即15(x2+y2+z2)+48(zx+xy+yz)≤21.
即15[(x+y+z)2-2(xy+xz+yz)]+48(xy+yz+zx)≤21,
∵x+y+z=1,∴即证明xy+yz+zx≤$\frac{1}{3}$.
由(x+y+z)2=x2+y2+z2+2(xy+yz+zx)≥3(xy+yz+zx),即可得出xy+yz+zx≤$\frac{1}{3}$成立.
因此原结论成立.
点评 本题考查了“分析法”、不等式的性质、乘法公式,考查了推理能力与计算能力,属于中档题.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案| 年龄/岁 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 合计 |
| 人数 | 8 | 40 | 231 | 315 | 280 | 107 | 13 | 6 | 1000 |
(1)年龄大于18岁的概率;
(2)年龄不低于15岁的概率.
| A. | 函数f(x)的值域为[0,4] | B. | 函数f(x)在[8,12]单调递增 | ||
| C. | 关于x的方程2f(x)-1=0有6个根 | D. | 不等式xf(x)≤6恒成立 |
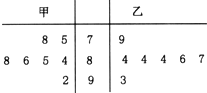 青年歌手大奖赛共有10名选手参赛,并请了7名评委,如茎叶图是7名评委给参加最后决赛的两位选手甲、乙评定的成绩,去掉一个最高分和一个最低分后,甲、乙选手剩余数据的平均成绩分别为84.2,85.
青年歌手大奖赛共有10名选手参赛,并请了7名评委,如茎叶图是7名评委给参加最后决赛的两位选手甲、乙评定的成绩,去掉一个最高分和一个最低分后,甲、乙选手剩余数据的平均成绩分别为84.2,85.