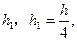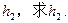题目内容
在棱长为a的正方体ABCD—A′B′C′D′中,E、F分别是BC、A′D′的中点.
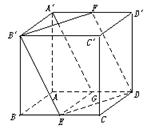
求证:四边形B′EDF是菱形;

求证:四边形B′EDF是菱形;
证明见解析
证明:如上图所示,由勾股定理,得B′E=ED=DF=FB′=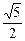 a,下证B′、E、
a,下证B′、E、
D、F四点共面,取AD中点G,连结A′G、EG,由EG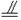 AB
AB A′B′知,B′EGA′是
A′B′知,B′EGA′是
平行四边形.∴B′E∥A′G,又A′F DG,∴A′GDF为平行四边形.
DG,∴A′GDF为平行四边形.
∴A′G∥FD,∴B′、E、D、F四点共面
故四边形B′EDF是菱形.
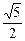 a,下证B′、E、
a,下证B′、E、D、F四点共面,取AD中点G,连结A′G、EG,由EG
 AB
AB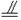 A′B′知,B′EGA′是
A′B′知,B′EGA′是平行四边形.∴B′E∥A′G,又A′F
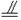 DG,∴A′GDF为平行四边形.
DG,∴A′GDF为平行四边形.∴A′G∥FD,∴B′、E、D、F四点共面
故四边形B′EDF是菱形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
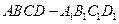 中,
中,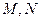 分别是
分别是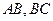 中点.
中点.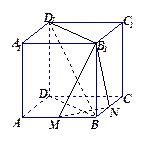
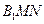 ⊥平面
⊥平面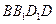 ;
;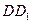 上有一点
上有一点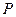 ,使
,使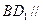 平面
平面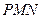 ,求
,求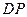 与
与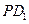 的比.
的比.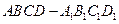 中,
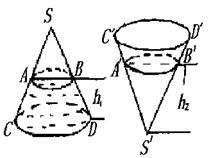
中,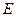 为
为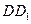 上的点、
上的点、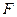 为
为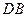 的中点.
的中点.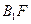 与平面
与平面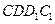 所成角的正弦值;
所成角的正弦值;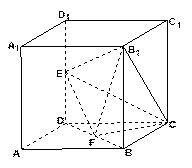 (Ⅱ)若直线
(Ⅱ)若直线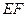 //平面
//平面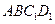 ,试确定点
,试确定点