题目内容
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,右焦点F是抛物线
,右焦点F是抛物线![]() :
:![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上
上![]()
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 已知斜率为k的直线l交椭圆
已知斜率为k的直线l交椭圆![]() 于A,B两点,
于A,B两点,![]() ,直线AM与BM的斜率乘积为
,直线AM与BM的斜率乘积为![]() ,若在椭圆上存在点N,使
,若在椭圆上存在点N,使![]() ,求
,求![]() 的面积的最小值.
的面积的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
![]() 先求出
先求出![]() 的值,即可求出
的值,即可求出![]() 的值,根据离心率求出
的值,根据离心率求出![]() 的值,即可得到椭圆方程
的值,即可得到椭圆方程
![]() 设直线
设直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
,![]() ,,由
,,由![]() ,根据直线
,根据直线![]() 与
与![]() 的斜率乘积为
的斜率乘积为![]() ,求出
,求出![]() ,再根据弦长公式求出
,再根据弦长公式求出![]() 和
和![]() ,表示出三角形的面积,再利用二次函数的性质即可求出最小值.
,表示出三角形的面积,再利用二次函数的性质即可求出最小值.
![]() 点
点![]() 在抛物线
在抛物线![]() 上,
上,
![]() ,
,
解得![]() ,
,
![]() 椭圆的右焦点为
椭圆的右焦点为![]() ,
,
![]() ,
,
![]() 椭圆
椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() ,
,
![]() 设直线l的方程为
设直线l的方程为![]() ,设
,设![]() ,
,![]() ,
,
由![]() ,消y可得
,消y可得![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,直线AM与BM的斜率乘积为
,直线AM与BM的斜率乘积为![]() ,
,
![]() ,
,
解得![]() ,
,
![]() 直线l的方程为
直线l的方程为![]() ,线段AB的中点为坐标原点,
,线段AB的中点为坐标原点,
由弦长公式可得![]() ,
,
![]() ,
,
![]() 垂直平分线段AB,
垂直平分线段AB,
当![]() 时,设直线ON的方程为
时,设直线ON的方程为![]() ,
,
同理可得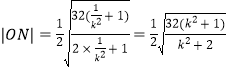 ,
,
![]() ,
,
当![]() 时,
时,![]() 的面积也适合上式,
的面积也适合上式,
令![]() ,
,![]() ,
,![]() ,
,
则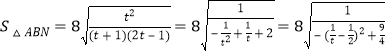 ,
,
![]() 当
当![]() 时,即
时,即![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
相关题目
【题目】某市化工厂三个车间共有工人1 000名,各车间男、女工人数如下表:
第一车间 | 第二车间 | 第三车间 | |
女工 | 173 | 100 | y |
男工 | 177 | x | z |
已知在全厂工人中随机抽取1名,抽到第二车间男工的可能性是0. 15.
(1)求x的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
【题目】据统计ABO血型具有民族和地区差异.在我国H省调查了30488人,四种血型的人数如下:
血型 | A | B | O | AB |
人数/人 | 7704 | 10765 | 8970 | 3049 |
频率 |
(1)计算H省各种血型的频率并填表(精确到0.001);
(2)如果从H省任意调查一个人的血型,那么他是O型血的概率大约是多少?