题目内容
已知函数f(x)=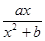 在x=1处取得极值2.
在x=1处取得极值2.
(1)求函数f(x)的表达式;
(2)当m满足什么条件时,函数f(x)在区间(m,2m+1)上单调递增?
(1)f(x)= ;(2)m∈(﹣1,0].
;(2)m∈(﹣1,0].
解析试题分析:(1)由已知可得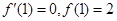 ,可得关于a,b的二元方程组,解此方程组可求得a,b的值.
,可得关于a,b的二元方程组,解此方程组可求得a,b的值.
(2)先利用导数求出f(x)的增区间,由条件可知(m,2m+1)为f(x)增区间的子集,从而可求得m所满足的条件.
试题解析:(1)因为f′(x)=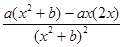 ,而函数f(x)=
,而函数f(x)=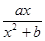 在x=1处取得极值2,所以
在x=1处取得极值2,所以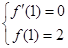 ,即
,即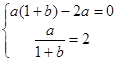 ,解得
,解得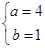 .
.
故f(x)= 即为所求.
即为所求.
(2)由(1)知f′(x)=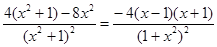 ,令f′(x)>0,得﹣1<x<1,∴f(x)的单调增区间为[﹣1,1].
,令f′(x)>0,得﹣1<x<1,∴f(x)的单调增区间为[﹣1,1].
由已知得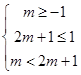 ,解得﹣1<m≤0.
,解得﹣1<m≤0.
故当m∈(﹣1,0]时,函数f(x)在区间(m,2m+1)上单调递增.
考点:1.函数的极值概念;2.利用导数研究函数的单调性.

练习册系列答案
相关题目
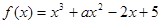
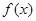 在
在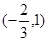 上单调递减,在
上单调递减,在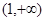 上单调递增,求实数
上单调递增,求实数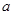 的值;
的值;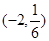 上单调递减,若存在,试求
上单调递减,若存在,试求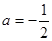 ,当
,当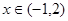 时不等式
时不等式 有解,求实数
有解,求实数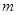 的取值范围.
的取值范围.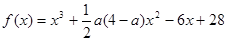 的导函数为
的导函数为 ,
,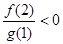 .求实数
.求实数 的取值范围。
的取值范围。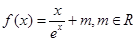 。
。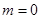 时,求
时,求 的单调区间、最大值;
的单调区间、最大值;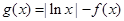 ,若存在实数
,若存在实数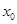 使得
使得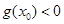 ,求m的取值范围。
,求m的取值范围。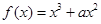 .
.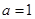 ,求函数
,求函数 的单调区间;
的单调区间;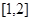 上是增函数,求
上是增函数,求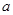 的取值范围.
的取值范围. ex,a,b
ex,a,b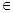 R,且a>0.
R,且a>0.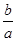 的取值范围.
的取值范围.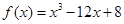 在区间
在区间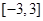 上的最大值与最小值分别为
上的最大值与最小值分别为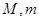 ,则
,则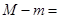 .
.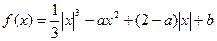 ,若
,若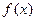 有六个不同的单调区间,
有六个不同的单调区间,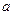 的取值范围为 ▲ .
的取值范围为 ▲ .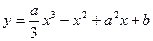 在点
在点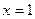 处存在极值
处存在极值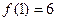 ,则
,则