题目内容
【题目】已知曲线![]() 的焦点是
的焦点是![]() ,
,![]() 、
、![]() 是曲线
是曲线![]() 上不同两点,且存在实数
上不同两点,且存在实数![]() 使得
使得![]() ,曲线
,曲线![]() 在点
在点![]() 、
、![]() 处的两条切线相交于点
处的两条切线相交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)点![]() 在
在![]() 轴上,以
轴上,以![]() 为直径的圆与
为直径的圆与![]() 的另一交点恰好是
的另一交点恰好是![]() 的中点,当
的中点,当![]() 时,求四边形
时,求四边形![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意知![]() 、
、![]() 、
、![]() 三点共线,可设直线
三点共线,可设直线![]() 的方程为
的方程为![]() ,并设点
,并设点![]() ,
,![]() ,将直线
,将直线![]() 的方程与曲线
的方程与曲线![]() 的方程联立,并列出韦达定理,利用导数求出曲线
的方程联立,并列出韦达定理,利用导数求出曲线![]() 在点
在点![]() 、
、![]() 处的切线方程,将两切线方程联立,求出点
处的切线方程,将两切线方程联立,求出点![]() 的坐标,即可得出点
的坐标,即可得出点![]() 的轨迹方程;
的轨迹方程;
(2)由![]() ,利用坐标运算得出
,利用坐标运算得出![]() ,代入韦达定理解出
,代入韦达定理解出![]() ,根据对称性取
,根据对称性取![]() ,求出线段
,求出线段![]() 的中点
的中点![]() 的坐标为
的坐标为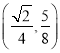 ,由
,由![]() 转化为
转化为![]() 可求出点
可求出点![]() 的坐标,并得出点
的坐标,并得出点![]() 的坐标,利用弦长公式计算出
的坐标,利用弦长公式计算出![]() ,利用点到直线的距离公式分别计算出
,利用点到直线的距离公式分别计算出![]() 和
和![]() 的高,并计算出这两个三角形的面积,相加即可得出四边形
的高,并计算出这两个三角形的面积,相加即可得出四边形![]() 的面积.
的面积.
(1)曲线![]() 就是抛物线
就是抛物线![]() ,它的焦点坐标为
,它的焦点坐标为![]() .
.
存在实数![]() 使得
使得![]() ,则
,则![]() 、
、![]() 、
、![]() 三点共线.
三点共线.
当直线斜率不存在时,不符合题意;
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,与
,与![]() 联立消去
联立消去![]() ,整理得
,整理得![]() ,判别式
,判别式![]() ,设
,设![]() ,
,![]() ,
,
则![]() 、
、![]() 就是方程
就是方程![]() 的两实根,
的两实根,![]() ,
,![]() .
.
![]() ,
,![]() ,切线斜率
,切线斜率![]() ,
,
则曲线![]() 在点
在点 处的切线方程是
处的切线方程是![]() ,即
,即![]() ①.
①.
同理得曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是![]() ②.
②.
联立①②得 ,得
,得 ,所以点
,所以点![]() 的坐标为
的坐标为![]() .
.
因此,点![]() 的轨迹方程为
的轨迹方程为![]() ;
;
(2)已知![]() ,在(1)的解答的基础上,
,在(1)的解答的基础上,
![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
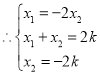 ,解得
,解得![]() ,
,![]() ,代入
,代入![]() 中,解得
中,解得![]() ,
,
注意到对称性,求四边形![]() 面积,只需取
面积,只需取![]() 即可.
即可.
![]() ,设
,设![]() 的中点为
的中点为![]() ,则
,则![]() ,
,![]() .
.
已知点![]() 在以点
在以点![]() 为直径的圆上,则
为直径的圆上,则![]() ,
,
设![]() ,由
,由![]() ,得
,得![]() ,即
,即 ,
,
解得![]() ,则
,则![]() .
.
将直线![]() 的方程
的方程![]() 化为
化为![]() ,
,
则点![]() 到
到![]() 的距离
的距离 .
.
所以![]() .
.
在(1)的解答中,联立①②消去![]() 解得
解得![]() ,
,
则两切线交点坐标为![]() ,
,
![]() 时,
时,![]() ,此时,点
,此时,点![]() 的坐标为
的坐标为 .
.
![]() 到
到![]() 的距离
的距离 .
.
所以![]() .
.
又已知![]() 、
、![]() 在
在![]() 两侧,所以
两侧,所以![]() .
.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案【题目】为考察某种药物预防疾病的效果,进行动物试验,调查了 105 个样本,统计结果为:服药的共有 55 个样本,服药但患病的仍有 10 个样本,没有服药且未患病的有 30个样本.
(1)根据所给样本数据完成 ![]() 列联表中的数据;
列联表中的数据;
(2)请问能有多大把握认为药物有效?
(参考公式:![]() 独立性检验临界值表
独立性检验临界值表
概率 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
患病 | 不患病 | 合计 | |
服药 | |||
没服药 | |||
合计 |
【题目】某地区实施“光盘行动”以后,某自助啤酒吧也制定了自己的行动计划,进店的每一位客人需预交![]() 元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足
元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足![]() 升的,按
升的,按![]() 升计算(如剩余
升计算(如剩余![]() 升,记为剩余
升,记为剩余![]() 升).例如:结账时,某桌剩余酒量恰好为
升).例如:结账时,某桌剩余酒量恰好为![]() 升,则该桌的每位客人还应付
升,则该桌的每位客人还应付![]() 元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的
元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的![]() 组数据
组数据![]() (其中
(其中![]() 表示饮酒人数,
表示饮酒人数,![]() (升)表示饮酒量):
(升)表示饮酒量):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
剩余酒量(单位:升) |
|
|
|
|
|
结账时的倍率 |
|
|
|
|
|
(1)求由这![]() 组数据得到的
组数据得到的![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)小王约了![]() 位朋友坐在一桌饮酒,小王及朋友用量杯共量取了
位朋友坐在一桌饮酒,小王及朋友用量杯共量取了![]() 升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请
升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请![]() 位或
位或![]() 位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
参考数据:回归直线的方程是![]() ,其中
,其中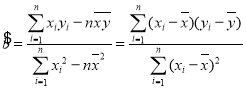 ,
,![]() .
.