题目内容
【题目】在平面直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线L:![]() ,曲线C的参数方程为
,曲线C的参数方程为![]() (
(![]() 为参数)
为参数)
![]() 求直线L和曲线C的普通方程;
求直线L和曲线C的普通方程;
![]() 在曲线C上求一点Q,使得Q到直线L的距离最小,并求出这个最小值
在曲线C上求一点Q,使得Q到直线L的距离最小,并求出这个最小值![]()
【答案】(1)直线L的普通方程为:![]() ;曲线C的普通方程为(x-5)2+y2=1;(2)点Q坐标为
;曲线C的普通方程为(x-5)2+y2=1;(2)点Q坐标为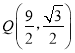 ,距离最小值为2.
,距离最小值为2.
【解析】
(1)根据极坐标与直角坐标的互化得到![]() 的普通方程,根据圆的参数方程相关知识得到
的普通方程,根据圆的参数方程相关知识得到![]() 的普通方程;(2)设出点的参数形式,利用点到直线的距离公式以及三角函数有界性计算点到直线距离的最小值.
的普通方程;(2)设出点的参数形式,利用点到直线的距离公式以及三角函数有界性计算点到直线距离的最小值.
解:(1)∵直线L:ρcosθ-![]() ρsinθ+1=0,
ρsinθ+1=0,
∴直线L的普通方程为:![]() ,
,
∵曲线C的参数方程为![]() (α为参数),
(α为参数),
∴曲线C的普通方程为(x-5)2+y2=1.
(2)设Q(5+cosα,sinα),Q到直线L的距离:
 ,
,
当![]() 时,即
时,即![]() ,dmin=2,
,dmin=2,
此时点Q坐标为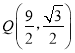 .
.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
【题目】某中学为研究学生的身体素质与体育锻炼时间的关系,对该校300名高三学生平均每天体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟).
平均每天锻炼的时间/分钟 |
|
|
|
|
|
|
总人数 | 34 | 51 | 59 | 66 | 65 | 25 |
将学生日均体育锻炼时间在![]() 的学生评价为“锻炼达标”.
的学生评价为“锻炼达标”.
(1)请根据上述表格中的统计数据填写下面的![]() 列联表;
列联表;
锻炼不达标 | 锻炼达标 | 合计 | |
男 | |||
女 | 40 | 160 | |
合计 |
(2)通过计算判断,是否能在犯错误的概率不超过0.05的前提下认为“锻炼达标”与性别有关?
参考公式:![]() ,其中
,其中![]() .
.
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |