Question

【题目】对于函数，如果存在实数（，且不同时成立），使得对恒成立，则称函数为“映像函数”.

（1）判断函数是否是“映像函数”，如果是，请求出相应的的值，若不是，请说明理由；

（2）已知函数是定义在上的“映像函数”，且当时，.求函数（）的反函数；

（3）在（2）的条件下，试构造一个数列，使得当时，，并求时，函数的解析式，及的值域．

Answer 1

【答案】（1）是“映像函数”，；（2）；（3），值域

【解析】

（1）直接由题意列关于a，b的方程组，求解得答案；

（2）由题意可得f（0）＝f（3），f（1）＝f（7），而当x∈[0，1）时，f（x）＝2x，则x∈[3，7）时，设f（x）＝2sx+t，可得，求得s，t的值，则函数解析式可求，把x用含有y的代数式表示，把x，y互换可得y＝f（x）（x∈[3，7））的反函数；

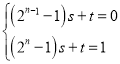（3）由（2）可知，构造数列{an}，满足a1＝0，an+1＝2an+1，可得数列{an+1}是以1为首项，以2为公比的等比数列，由此求得．当x∈[an，an+1）＝[2n﹣1﹣1，2n﹣1），令，解得s＝21﹣n，t＝21﹣n﹣1，可得x∈[an，an+1）（n∈N*）时，函数y＝f（x）的解析式为f（x），并求得x∈[0，+∞）时，函数f（x）的值域为[1，2）．

（1）对于，，

若，则，

即恒成立，∴，∵不同时成立，∴，

即是“映像函数”

（2）当时，，从而，∵函数是定义在上的“映像函数”，

∴，令，则，∴

∴（），由得，，此时

∴当时，函数的反函数是；

（3）∵时，，

∴构造数列，，且，于是，

∴是以为首项，为公比的等比数列，∴，

而

∴当，即时，

对于函数，∵，令，则

∴，

∴当时，，

函数在上单调递增，∴

而，

即函数的值域为.