题目内容
(本小题满分12分)一动圆与已知 :
: 相外切,与
相外切,与 :
: 相内切.
相内切.
(Ⅰ)求动圆圆心的轨迹C;
(Ⅱ)若轨迹C与直线y="kx+m" (k≠0)相交于不同的两点M、N,当点A(0,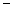 1)满足|
1)满足|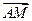 |=|
|=| | 时,求m的取值范围.
| 时,求m的取值范围.
 :
: 相外切,与
相外切,与 :
: 相内切.
相内切.(Ⅰ)求动圆圆心的轨迹C;
(Ⅱ)若轨迹C与直线y="kx+m" (k≠0)相交于不同的两点M、N,当点A(0,
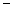 1)满足|
1)满足|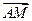 |=|
|=| | 时,求m的取值范围.
| 时,求m的取值范围.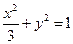 ,
,
(Ⅰ)设动圆圆心为M(x , y),半径为R,则由题设条件,可知:
|MO1|="1+R" ,|MO2|=(2 )
)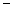 R, ∴|MO1|+|MO2|=2
R, ∴|MO1|+|MO2|=2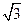 .
.
由椭圆定义知:M在以O1,O2为焦点的椭圆上,且 ,
, ,
,
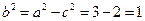 ,故动圆圆心的轨迹方程为
,故动圆圆心的轨迹方程为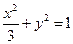 .…………………4分
.…………………4分
(Ⅱ)设P为MN的中点,联立方程组 ,
,
 (3k2+1)x2+6mkx+3(m2
(3k2+1)x2+6mkx+3(m2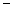 1)=0.
1)=0.
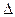 =
=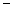 12m2+36k2+12>0
12m2+36k2+12>0 m2<3k2+1 …………………… (1) ………………6分
m2<3k2+1 …………………… (1) ………………6分
又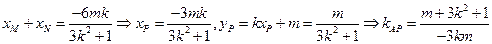
由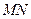 ⊥
⊥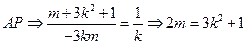 …………(2) ……………9分
…………(2) ……………9分
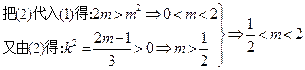 .故
.故 .…………12分高&考%
.…………12分高&考%
|MO1|="1+R" ,|MO2|=(2
 )
)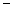 R, ∴|MO1|+|MO2|=2
R, ∴|MO1|+|MO2|=2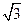 .
.由椭圆定义知:M在以O1,O2为焦点的椭圆上,且
 ,
, ,
,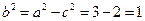 ,故动圆圆心的轨迹方程为
,故动圆圆心的轨迹方程为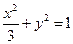 .…………………4分
.…………………4分(Ⅱ)设P为MN的中点,联立方程组
 ,
, (3k2+1)x2+6mkx+3(m2
(3k2+1)x2+6mkx+3(m2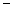 1)=0.
1)=0.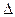 =
=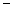 12m2+36k2+12>0
12m2+36k2+12>0 m2<3k2+1 …………………… (1) ………………6分
m2<3k2+1 …………………… (1) ………………6分又
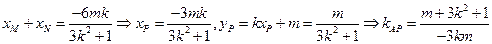
由
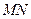 ⊥
⊥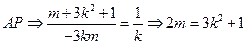 …………(2) ……………9分
…………(2) ……………9分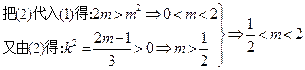 .故
.故 .…………12分高&考%
.…………12分高&考%
练习册系列答案
相关题目
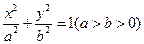 的左焦点为
的左焦点为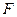 ,左右顶点分别为
,左右顶点分别为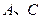 ,上顶点为
,上顶点为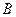 ,过
,过 三点作圆
三点作圆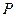 ,其中圆心
,其中圆心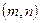 .
. 时,椭圆的离心率的取值范围.
时,椭圆的离心率的取值范围.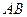 能否和圆
能否和圆
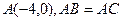 ,且
,且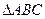 的内切圆方程为
的内切圆方程为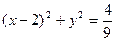 .
. 三点的椭圆标准方程;
三点的椭圆标准方程; 作圆的切线,求切线长最短时的点
作圆的切线,求切线长最短时的点 满足
满足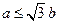 ,离心率为
,离心率为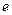 ,则
,则 的最大值是_______.
的最大值是_______.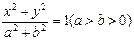 的短轴位于x轴下方的端点,过B作斜率为1的直线交椭圆于点M,点P在y轴上,且PM//x轴,
的短轴位于x轴下方的端点,过B作斜率为1的直线交椭圆于点M,点P在y轴上,且PM//x轴,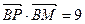 ,若点P的坐标为(0,t),则t的取值范围是 ( )
,若点P的坐标为(0,t),则t的取值范围是 ( )
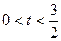
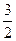
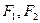 分别是椭圆
分别是椭圆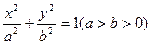 的左、右焦点,上顶点为M。若在椭圆上存在一点P,分别连结PF1,PF2交y轴于A,B两点,且满足
的左、右焦点,上顶点为M。若在椭圆上存在一点P,分别连结PF1,PF2交y轴于A,B两点,且满足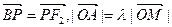 ,则实数
,则实数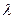 的取值范围为 。
的取值范围为 。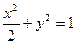 的右焦点为F,右准线为l,点
的右焦点为F,右准线为l,点 ,线段AF交椭圆C于点B,若
,线段AF交椭圆C于点B,若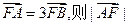 =" " ( )
=" " ( )
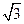
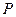 是椭圆
是椭圆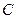 :
: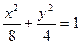 上的动点,
上的动点,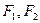 分别为左、右焦点,
分别为左、右焦点,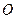 为坐标原点,则
为坐标原点,则 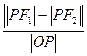 的取值范围是 ( )
的取值范围是 ( )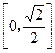

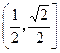
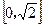
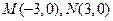 ,若直线上存在点P,使得
,若直线上存在点P,使得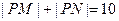 ,则称该直线为“A型直线”。给出下列直线:①
,则称该直线为“A型直线”。给出下列直线:① ;②
;②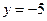 ;③
;③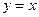 ;④
;④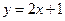 ,其中是“A型直线”的是
,其中是“A型直线”的是