题目内容
已知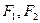 分别是椭圆
分别是椭圆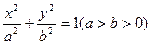 的左、右焦点,上顶点为M。若在椭圆上存在一点P,分别连结PF1,PF2交y轴于A,B两点,且满足
的左、右焦点,上顶点为M。若在椭圆上存在一点P,分别连结PF1,PF2交y轴于A,B两点,且满足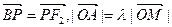 ,则实数
,则实数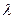 的取值范围为 。
的取值范围为 。
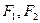 分别是椭圆
分别是椭圆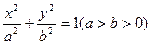 的左、右焦点,上顶点为M。若在椭圆上存在一点P,分别连结PF1,PF2交y轴于A,B两点,且满足
的左、右焦点,上顶点为M。若在椭圆上存在一点P,分别连结PF1,PF2交y轴于A,B两点,且满足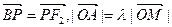 ,则实数
,则实数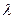 的取值范围为 。
的取值范围为 。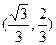
略

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
题目内容
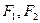 分别是椭圆
分别是椭圆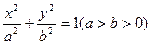 的左、右焦点,上顶点为M。若在椭圆上存在一点P,分别连结PF1,PF2交y轴于A,B两点,且满足
的左、右焦点,上顶点为M。若在椭圆上存在一点P,分别连结PF1,PF2交y轴于A,B两点,且满足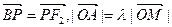 ,则实数
,则实数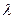 的取值范围为 。
的取值范围为 。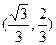

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案