题目内容

如图,已知点
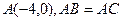 ,且
,且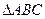 的内切圆方程为
的内切圆方程为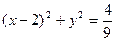 .
.(1) 求经过
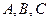 三点的椭圆标准方程;
三点的椭圆标准方程;(2) 过椭圆上的点
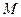 作圆的切线,求切线长最短时的点
作圆的切线,求切线长最短时的点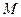 的坐标和切线长。
的坐标和切线长。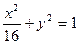 ,
,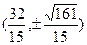
解:(Ⅰ)设椭圆的标准方程为 ,------------------1分
,------------------1分
依题意知直线AB的斜率存在,故设直线AB:y=k(x+4) ------------------2分
------------------2分
因圆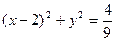 的圆心为(2,0),半径
的圆心为(2,0),半径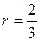 ,又因为直线AB与圆相切
,又因为直线AB与圆相切
所以,圆心为(2,0)到直线AB的距离为 ------------------3分
------------------3分
解得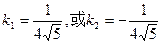 (
(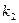 为直线AC的斜率)
为直线AC的斜率)
所以直线AB的方程为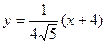 ,------------------4分
,------------------4分
又因为AB=AC,点A(-4,0)在x轴上,所以B点横坐标为 ,
,
把 代入直线AB的方程解得
代入直线AB的方程解得 ,
,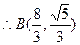 ------------------5分
------------------5分
把A(-4,0),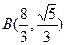 代入椭圆方程得
代入椭圆方程得 ,解得m=16,
,解得m=16, n=1----------6分
n=1----------6分
所以椭圆的标准方程为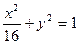 .------------------
.------------------ 7分
7分
(Ⅱ)设点M ,则圆心(2,0)与点M的距离为
,则圆心(2,0)与点M的距离为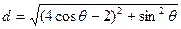 -8分
-8分
切线长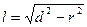 ,
,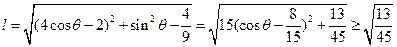 ,--10分
,--10分
当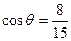 时,
时, , ------------------12分
, ------------------12分
此时 ,从而点
,从而点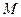 的坐标为
的坐标为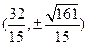 ------------------14分
------------------14分
解法二:(Ⅰ)因为AB=AC,点A(-4,0)在x轴上,且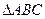 的内切圆方程为
的内切圆方程为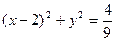 ,
,
 所以B点横坐标为
所以B点横坐标为 ,-----------------1分
,-----------------1分
如图,由三角形内切圆的性质知 ∽
∽
∴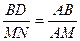 即
即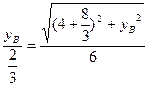 ,从而
,从而
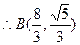 ------------------3分
------------------3分
当椭圆的焦点在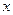 轴上时,设椭圆方程为
轴上时,设椭圆方程为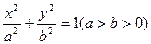 ,则将A(-4,0),
,则将A(-4,0),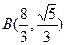 代入椭圆方程得
代入椭圆方程得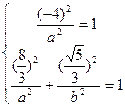 ,解得
,解得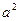 =16,
=16,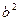 ="1" ,
="1" ,
∴椭圆的标准方程为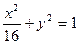 --5分
--5分
当椭圆的焦点在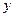 轴上时,设椭圆方程为
轴上时,设椭圆方程为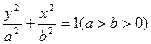 ,则将A(-4,0),
,则将A(-4,0),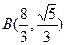 代入椭圆方程得
代入椭圆方程得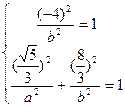 ,解得
,解得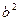 =16,
=16,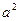 =
=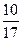 与
与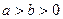 矛盾----------6分
矛盾----------6分
综上所述,所求椭圆的标准方程为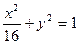 .------------------7分
.------------------7分
(Ⅱ) 依题意设点M ,则圆心(2,0)与点M
,则圆心(2,0)与点M 的距离为
的距离为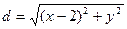 ------8分
------8分
则切线长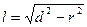 ,而
,而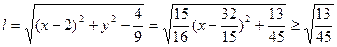 ,---------10分
,---------10分
当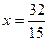 时,
时, ,-----12分
,-----12分
此时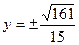 ,从而点
,从而点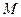 的坐标为
的坐标为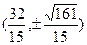 -----14分
-----14分
 ,------------------1分
,------------------1分依题意知直线AB的斜率存在,故设直线AB:y=k(x+4)
 ------------------2分
------------------2分因圆
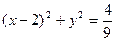 的圆心为(2,0),半径
的圆心为(2,0),半径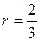 ,又因为直线AB与圆相切
,又因为直线AB与圆相切所以,圆心为(2,0)到直线AB的距离为
 ------------------3分
------------------3分解得
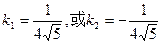 (
(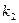 为直线AC的斜率)
为直线AC的斜率)所以直线AB的方程为
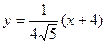 ,------------------4分
,------------------4分又因为AB=AC,点A(-4,0)在x轴上,所以B点横坐标为
 ,
,把
 代入直线AB的方程解得
代入直线AB的方程解得 ,
,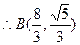 ------------------5分
------------------5分把A(-4,0),
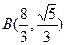 代入椭圆方程得
代入椭圆方程得 ,解得m=16,
,解得m=16, n=1----------6分
n=1----------6分所以椭圆的标准方程为
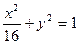 .------------------
.------------------ 7分
7分(Ⅱ)设点M
 ,则圆心(2,0)与点M的距离为
,则圆心(2,0)与点M的距离为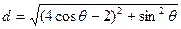 -8分
-8分切线长
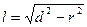 ,
,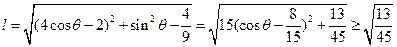 ,--10分
,--10分当
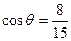 时,
时, , ------------------12分
, ------------------12分此时
 ,从而点
,从而点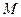 的坐标为
的坐标为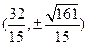 ------------------14分
------------------14分解法二:(Ⅰ)因为AB=AC,点A(-4,0)在x轴上,且
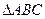 的内切圆方程为
的内切圆方程为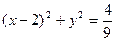 ,
, 所以B点横坐标为
所以B点横坐标为 ,-----------------1分
,-----------------1分如图,由三角形内切圆的性质知
 ∽
∽
∴
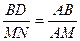 即
即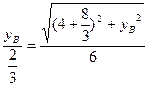 ,从而
,从而
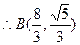 ------------------3分
------------------3分当椭圆的焦点在
 轴上时,设椭圆方程为
轴上时,设椭圆方程为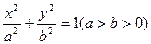 ,则将A(-4,0),
,则将A(-4,0),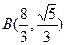 代入椭圆方程得
代入椭圆方程得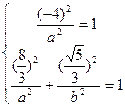 ,解得
,解得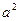 =16,
=16,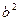 ="1" ,
="1" ,∴椭圆的标准方程为
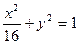 --5分
--5分当椭圆的焦点在
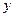 轴上时,设椭圆方程为
轴上时,设椭圆方程为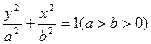 ,则将A(-4,0),
,则将A(-4,0),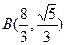 代入椭圆方程得
代入椭圆方程得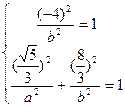 ,解得
,解得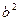 =16,
=16,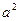 =
=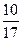 与
与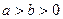 矛盾----------6分
矛盾----------6分综上所述,所求椭圆的标准方程为
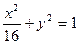 .------------------7分
.------------------7分(Ⅱ) 依题意设点M
 ,则圆心(2,0)与点M
,则圆心(2,0)与点M 的距离为
的距离为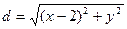 ------8分
------8分则切线长
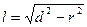 ,而
,而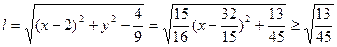 ,---------10分
,---------10分当
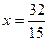 时,
时, ,-----12分
,-----12分此时
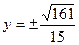 ,从而点
,从而点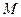 的坐标为
的坐标为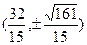 -----14分
-----14分
练习册系列答案
相关题目
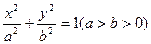 的长轴
的长轴 ,离心率
,离心率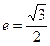 ,
, 为坐标原点,过
为坐标原点,过 的直线
的直线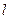 与
与 轴垂直,
轴垂直,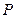 是椭圆上异于
是椭圆上异于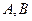 的任意一点,
的任意一点,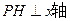 ,
,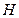 为垂足,延长
为垂足,延长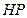 至
至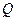 ,使得
,使得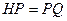 ,连接
,连接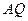 并延长交直线
并延长交直线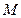 ,
,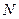 为
为 的中点
的中点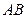 为直径的圆
为直径的圆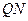 与圆
与圆
 :
: 相外切,与
相外切,与 :
: 相内切.
相内切. 1)满足|
1)满足|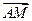 |=|
|=| | 时,求m的取值范围.
| 时,求m的取值范围.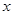 轴上的椭圆
轴上的椭圆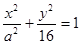 的两个焦点分别为
的两个焦点分别为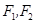 , 且
, 且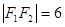 ,弦
,弦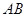 过焦点
过焦点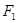 ,则
,则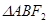 的周长为
的周长为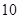
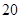
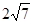

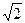 ,BC=1.以AB的中点
,BC=1.以AB的中点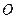 为原点建立如图8所示的平面直角坐标系
为原点建立如图8所示的平面直角坐标系 .
.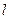 交(Ⅰ)中椭圆于M,N两点,是否存在直线
交(Ⅰ)中椭圆于M,N两点,是否存在直线
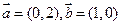 ,过定点
,过定点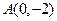 ,以
,以 方向向量的直线与经过点
方向向量的直线与经过点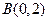 ,以向量
,以向量 为方向向量的直线相交于点P,其中
为方向向量的直线相交于点P,其中
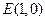 的直线
的直线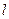 与C交于两个不同点M、N,求
与C交于两个不同点M、N,求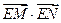 的取值范围
的取值范围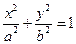 (a>b>0)的离心率为
(a>b>0)的离心率为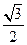 ,过右焦点F且斜率为k(k>0)的直线于C相交于A、B两点,若
,过右焦点F且斜率为k(k>0)的直线于C相交于A、B两点,若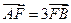 。则k =
。则k =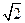 (C)
(C)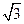 (D)2
(D)2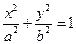
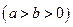 ,当
,当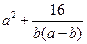 的最小值时,椭圆的离心率
的最小值时,椭圆的离心率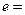 .
.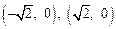 ,则PC·PD的最大值为 .
,则PC·PD的最大值为 .