题目内容
【题目】现有一张长为![]() ,宽为
,宽为![]() (
(![]() )的长方形铁皮
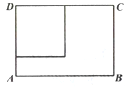
)的长方形铁皮![]() ,准备用它做成一个无盖长方体铁皮容器,要求材料利用率为100%,不考虑焊接处损失.如图,在长方形
,准备用它做成一个无盖长方体铁皮容器,要求材料利用率为100%,不考虑焊接处损失.如图,在长方形![]() 的一个角上剪下一块边长为
的一个角上剪下一块边长为![]() 的正方形铁皮,作为铁皮容器的底面,用余下材料剪拼后作为铁皮容器的侧面,设长方体的高为
的正方形铁皮,作为铁皮容器的底面,用余下材料剪拼后作为铁皮容器的侧面,设长方体的高为![]() ,体积为
,体积为![]() .
.
(Ⅰ)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)求该铁皮容器体积![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() (
(![]() ).(Ⅱ)
).(Ⅱ)
【解析】试题分析:(1)根据一张长为![]() ,宽为
,宽为![]() 的长方形铁皮
的长方形铁皮![]() 可得
可得![]() ,进而可确定
,进而可确定![]() 与
与![]() 的关系式;
的关系式;
(2)铁皮盒体积![]()
求导函数,分类讨论,确定函数的极值,极大值,也是最大值.
试题解析:((Ⅰ)由题意得![]() ,
,
即![]() (
(![]() ).
).
(Ⅱ)铁皮容器体积![]()
![]() (
(![]() ).
).
![]()
![]() ,
,
当![]() 时,即
时,即![]() ,在
,在![]() 上,
上, ![]() 恒成立,函数
恒成立,函数![]() 单调递增,
单调递增,
此时![]() ;
;
当![]() ,即
,即![]() ,在
,在![]() 上,
上, ![]() ,函数
,函数![]() 单调递增,在
单调递增,在![]() 上,
上, ![]() ,函数
,函数![]() 单调递减,此时
单调递减,此时![]() .
.
所以

 阅读快车系列答案
阅读快车系列答案【题目】在某次电影展映活动中,展映的影片有科幻片和文艺片两种类型,统计一随机抽样调查的样本数据显示,100名男性观众中选择科幻片的有60名,女性观众中有![]() 的选择文艺片,选择文艺片的观众中男性观众和女性观众一样多.
的选择文艺片,选择文艺片的观众中男性观众和女性观众一样多.
(Ⅰ)根据以上数据完成下列![]() 列联表
列联表

(Ⅱ)能否在犯错误的概率不超过0.01的前提下,认为选择影片类型与性别有关?
附:
| … | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| … | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |

【题目】某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的60名学生中有45人比较细心,另外15人比较粗心;在数学成绩不及格的40名学生中有10人比较细心,另外30人比较粗心.
(1)试根据上述数据完成![]() 列联表;
列联表;
数学成绩及格 | 数学成绩不及格 | 合计 | |
比较细心 | 45 | ||
比较粗心 | |||
合计 | 60 | 100 |
(2)能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系?
参考数据:独立检验随机变量![]() 的临界值参考表:
的临界值参考表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中![]()
【题目】某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的60名学生中有45人比较细心,另外15人比较粗心;在数学成绩不及格的40名学生中有10人比较细心,另外30人比较粗心.
(1)试根据上述数据完成![]() 列联表;
列联表;
数学成绩及格 | 数学成绩不及格 | 合计 | |
比较细心 | 45 | ||
比较粗心 | |||
合计 | 60 | 100 |
(2)能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系?
参考数据:独立检验随机变量![]() 的临界值参考表:
的临界值参考表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中![]()